In Kapitel 8 hatten wir die Basis-Kennzahlen festgelegt, die wir nachfolgend von der chess engine Stockfish für jede einzelne Schachstellung unserer analysierten Spiele berechnen ließen und in der Datenbank-Tabelle position_analysis gespeichert haben.
Wie bereits angekündigt, wollen wir davon weitere Kennzahlen ableiten, die ebenfalls in unserer Datenbank gespeichert werden sollen. Einige davon ergeben sich durch bloße numerische Umrechnung aus den Basis-Kennzahlen, andere durch Vergleiche der Bewertungen von jeweils einer Ausgangs-Position mit der entstandenen Ziel-Position nach einem ausgeführten Zug.
Wieder andere Kennzahlen wie z.B. ACPL sind als Durchschnittswerte statistischer Natur, auf eine gesamte Partie bezogen und daher Positions-übergreifend.
Wie erwähnt interessieren uns letztlich Messdaten für ausgewählte Spieler und deren Vergleich untereinander. Wir nutzen also unsere Positions-Kennzahlen zur Partien- und nachfolgend der Spieler-Bewertung.
Wir werden daher auf allen drei Ebenen Spieler, Partien und Positionen Werte berechnen. Demzufolge benötigen wir zu deren Speicherung weitere Tabellen in genau dieser Hierarchie (das Tabellenprefix ‚da‘ steht für engl. derived analytics).
Werfen wir zur Veranschaulichung nochmals einen Blick auf unsere bereits ermittelten Basis-Kennzahlen aus der Stockfish-Analyse. Wir betrachten dazu ein konkretes Spiel mit sämtlichen analysierten Postitionen anhand unserer Daten
.

Im oberen Bereich des Bildes sehen wir unsere SQL-Abfrage, mit der wir hier die für unseren Zweck wesentlichen Daten ermitteln.
- ) In der Spalte fen sind die einzelnen Schachpositionen kodiert, auf die sich die Kennzahlen wie centipawn beziehen. Zur FEN-Dekodierung und Anzeige der zugehörigen Position kann der Chess FEN Viewer benutzt werden.
- ) die Werte in der Spalte half_move_num sind aufsteigend nach Halbzug-Nummer sortiert. Für die Züge vor dem fünften Halbzug liegen keine Analyse-Ergebnisse vor. Offenbar handelt es sich dabei um bekannte Stellungen, die wir ja bewusst von einer Bewertung ausgeschlossen hatten.
- ) In den beiden Spalten move_white bzw. move_black befinden sich die einzelnen Züge, die zur bewerteten Position geführt haben.
- ) in der Spalte best_move_uci findet sich der aus Sicht der chess engine vorgeschlagene beste Zug aus dieser Position heraus.
- und 6. ) In der Schachposition von Zeile 7 wurde e5e4 als bester Zug (aus Sicht der engine) ermittelt. In Zeile 8 sehen wir, dass dieser Zug in der Partie von Schwarz tatsächlich auch ausgeführt wurde. Gleichzeitig wird damit verständlich, dass wir bestimmte Kennzahlen wie accuracy, welche ja aus der Differenz beider Bewertungen berechnet wird, nur durch Positions-übergreifende Betrachtung ermitteln können!
Abgeleitete Kennzahlen auf Positions-Ebene
Gehen wir der Reihe nach vor. Aus den Basis-Kennzahlen centipawn, wins, draws und losses, die wir aus der Partien-Analyse gewonnen haben, können wir direkt weitere Kennzahlen ableiten, die auf der Ebene der betreffenden Stellung bzw. des durchgeführten Zuges angesiedelt sind.
Hier nur ein Überblick – die konkrete Implementierung wird später gezeigt.
- White/Black winning chances
Die Gewinnwahrscheinlichkeit für eine Seite (Weiß oder Schwarz) kann direkt aus der Kennzahl centipawns abgeleitet werden.
Die genaue Formel für Win% wurde auf lichess.org definiert. - White/Black score rate
Die Score-Rate gibt die Wahrscheinlichkeit an, einen Punkt zu erzielen. Da es im Schach bei einem Unentschieden (remis) zu einer Punkteteilung kommt, ist dieser Fall ebenso zu berücksichtigen. Die Score-Rate kann direkt aus den WDL-Werten berechnet werden. - White/Black draw rate
Diese Kennzahl wird ebenfalls aus den WDL-Werten berechnet und gibt die Wahrscheinlichkeit für ein Remis ausgehend von der gegebenen Stellung an. - Accuracy (Zuggenauigkeit)
Die Genauigkeit bezeichnet den Grad der Abweichung des durchgeführten Zuges vom optimalen Zug aus Sicht der chess engine. Hierzu sind jeweils zwei aufeinanderfolgende Zeilen (Halbzüge) der Tabelle position_analysis zu berücksichtigen. Dabei wird die Gewinnwahrscheinlichkeit für die Ausgangsstellung (unter der Annahme, dass der optimale Zug gemacht wird) mit der Gewinnwahrscheinlichkeit für die Folgestellung, die durch den realen Spielzug entstanden ist, verglichen. Damit ist auch klar, dass jeweils für die erste Zeile der Tabelle position_analysis pro Partie der Wert accuracy nicht definiert ist! - Judgement (Zug-Klassifikation)
Die Kennzahl judgement soll die Qualität eines Zuges grob bewerten, um sie im Vergleich zur rein numerischen Kennzahl accuracy zu veranschaulichen. Die Kennzahl judgment kann vier verschiedene Werte annehmen, die über festgelegte Schwellwerte von der Kennzahl accuracy abgeleitet werden:- „ENGINE„
der durchgeführte Zug entspricht dem optimalen, von der engine vorgeschlagenen Zug. - „INACCURACY„
der durchgeführte Zug entspricht nicht dem optimalen Zug, kann aber auch noch nicht als klarer Fehler bezeichnet werden. - „MISTAKE„
ein klar schlechter Zug aus Sicht der engine. - „BLUNDER„
ein schwer wiegender Fehler („Patzer“) aus Sicht der engine.
- „ENGINE„
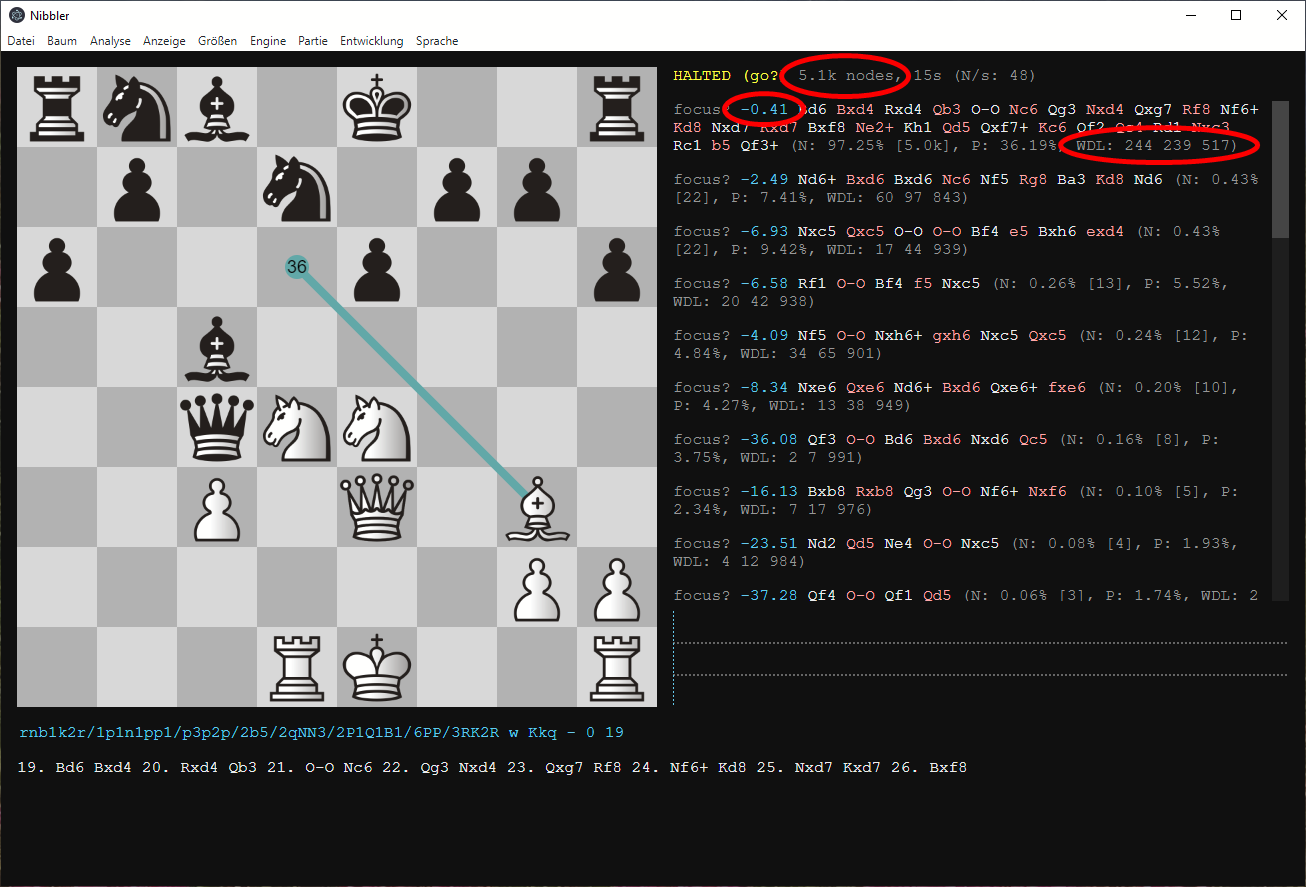
Vergleichen wir nun exakt dieselbe Stellung mit der Bewertung durch Stockfish, erwarten wir aufgund der ebenbürtigen Spielstärke der beiden engines ähnliche Werte.
c:\git_projects\chessAnalyzer\various python scripts>python analyse_Caruana-Vachier-Lagrave_2021_move_19.py
r n b . k . . r
. p . n . p p .
p . . . p . . p
. . b . . . . .
. . q N N . . .
. . P . Q . B .
. . . . . . P P
. . . R K . . R
centipawn: -24
wins: 7
draws: 947
losses: 46
c:\git_projects\chessAnalyzer\various python scripts>Unberücksichtigte Kennzahlen
Es gibt viele weitere interessante Merkmale, Schachstellungen oder einzelne Züge betreffend, die wir hier nur der Vollständigkeit halber erwähnen wollen. Sie sind entweder nicht klar definiert, kompliziert zu berechnen oder zu wenig relevant zur Beurteilung der Stärke eines Spielers.
- Brillanz
Solch ein Zug muss nach allgemeinem Verständnis der stärkste mögliche Zug sein. Dazu darf er nicht offensichtlich sein, sondern muss eine gewisse Tiefe aufweisen, die in einer überraschenden Pointe mündet.
Der Zug muss nicht unbedingt zum Sieg führen, aber ob damit ein Figurenopfer verbunden sein soll, daran scheiden sich bereits die Geister! Dazu lassen sie sich als taktisch oder strategisch brillante Züge kategorisieren. Die Diskussionen um die richtige Einordnung halten jedenfalls weiter an. - heat map
Es geht dabei im Prinzip um den Vergleich, welche Seite mehr Felder auf dem Spielbrett kontrolliert. Der Begriff „heat map“ leitet sich davon ab, dass diese Felder anhand ihres Status (von Weiß/Schwarz kontrolliert, neutral, umstritten) leicht visuell dargestellt werden können. Natürlich ließe sich das auch in eine Kennzahl umrechnen. - peace activity
gemäß Paul Morphy’s Leitsatz „Hilf deinen Figuren, damit sie dir helfen“ ist Figurenaktivität sicher eine der interessanteren Kennzahlen, vergleiche etwa hier. Allerdings berücksichtigt eine chess engine dieses Merkmal bereits in seiner internen Stellungsbewertung. Wir sehen daher von einer gesonderten Betrachtung ab. - Stellungskomplexität
Dass eine übersichtlichere Stellung leichter zu spielen ist, liegt auf der Hand. Dementsprechend ist es viel schwieriger, in einer sehr komplizierten Stellung mit vielen Figuren auf dem Brett und gespickt mit taktischen Fallen, Drohungen und Fesselungen, einen guten Zug zu finden. Daher klingt die Aufgabe, komplexe Stellungen als solche zu identifizieren, bereits äußerst kompliziert!
Ein interessanter Ansatz, relativ einfach zumindest ein starkes Indiz für eine komplizierte Stellung zu finden, wurde in einem Artikel von Matej Guid und Ivan Bratko beschrieben.
Demnach lassen sich komplizierte Stellungen auch dadurch charakterisieren, indem man die Bewertungen der besten Züge bei unterschiedlichen Suchtiefen ermittelt. Sind diese Einzelbewertungen nun starken Schwankungen unterworfen, kann daraus geschlossen werden, dass die untersuchte Stellung auf jeden Fall schwer einzuschätzen ist, was wiederum eine plausible Definition für eine komplizierte Stellung sein kann.
Wir wollen diesen Gedanken nicht weiter vertiefen, auch weil damit weiterer Rechenaufwand und damit zusätzliche Rechenzeit verbunden sind.
Zwischenfazit
Wir haben nun die abgeleiteten Kennzahlen auf Positionsebene definiert, die wir in einer eigenen Datenbank-Tabelle speichern werden. Die zugehörigen Werte leiten sich von den Basis-Kennzahlen ab. Somit entsteht aus jedem Datensatz der Tabelle position_analysis ein zugehöriger Datensatz in einer neuen Tabelle, die wir da_position nennen (das Präfix „da“ steht für „derived analytics“, wie oben erwähnt). Im Gegensatz zu den mit viel Rechenaufwand von Stockfish ermittelten Analyse-Kennzahlen sind die abgeleiteten Kennzahlen in wenigen Minuten berechnet. Deshalb speichern wir diese auch in einer separaten Tabelle, die wir jederzeit erweitern, ggf. korrigieren und neu berechnen lassen können können.
Implementierung
Als Erstes erstellen wir die Tabelle da_position mit den abgeleiteten Kennzahlen. Jede Zeile dieser Tabelle steht in einer eindeutigen Beziehung zu einer bestimmten Spielstellung und deren Basis-Kennzahlen. Dementsprechend erfolgt die Fremdschlüssel-Verknüpfung über die Spalte position.id wie unten dargestellt.
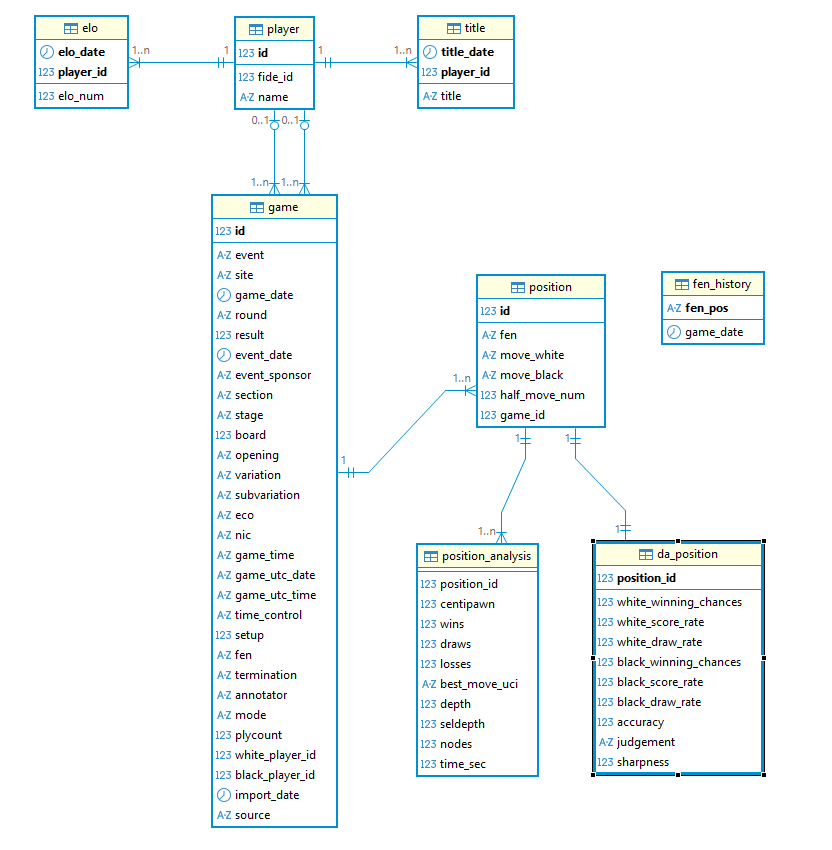
Da die Berechnung der abgeleiteten Kennzahlen mathematisch relativ simpel und die Programmlogik Datenbank-zentriert ist, verwenden wir statt PythonPL/SQL-Code. und schreiben ein Package da, das den gesamten Code für alle abgeleiteten Kennzahlen enthalten soll. Momentan enthält es nur Code zur Berechnung der Positions-bezogenen abgeleiteten Kennzahlen. Zusätzlich erstellen wir ein Hilfs-PL/SQL-Package für ein Logging und eine zugehörige Logtabelle, in die wir ggf. Fehler- und Diagnose-Daten schreiben. Da MariaDB nicht über eine autonome Commit-Funktion wie z.B. Oracle verfügt und wir das Logging aber vom Transaktionsverhalten der eigentlichen Programmlogik entkoppeln wollen, verwenden wir für die Tabelle logtable die spezielle MariaDB engine Aria. Damit bleiben die Fehlermeldungen auch dann erhalten, falls die Speicherung der abgeleiteten Kennzahlen aufgrund eines Problems nicht erfolgen kann.
CREATE TABLE `logtable` (
`id` bigint(20) NOT NULL AUTO_INCREMENT,
`dat` datetime NOT NULL DEFAULT current_timestamp(),
`msg` varchar(2000) DEFAULT NULL,
PRIMARY KEY (`id`)
) ENGINE=Aria DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_general_ci CHECKSUM=1 PAGE_CHECKSUM=1 TRANSACTIONAL=1;Log-Tabelle logtable
SET SESSION SQL_MODE='ORACLE';
DELIMITER //
CREATE DEFINER="chess_user"@"%" PACKAGE "logging" AS
-- must be declared as public!
PROCEDURE log(p_msg IN varchar2);
END
//
CREATE DEFINER="chess_user"@"%" PACKAGE BODY "logging" as
procedure log(p_msg IN varchar2)
as
begin
insert into logtable (msg) values (p_msg);
end log;
end
//LOGGING Package Spezifikation und Body
PL/SQL Code
SET SESSION SQL_MODE='ORACLE';
DELIMITER //
CREATE OR REPLACE PACKAGE da AS
-- must be declared as public!
PROCEDURE gen_da_position(p_player_id NUMBER(20));
procedure gen_da_game;
END da;
//
CREATE OR REPLACE PACKAGE BODY da as
function calc_win_percent(p_centipawns in double) return double
as
v_win_percent double;
begin
v_win_percent := 50.0 + 50.0 * (2.0 / (1.0 + exp(-0.00368208 * p_centipawns)) - 1.0);
return v_win_percent;
end calc_win_percent;
function calc_accuracy (p_winpercent_before in double, p_winpercent_after in double) return double
as
v_win_diff double;
v_accuracy double;
begin
if p_winpercent_after >= p_winpercent_before then
return (100.0);
end if;
v_win_diff := p_winpercent_before - p_winpercent_after;
v_accuracy := 103.1668 * exp(-0.04354 * (v_win_diff)) - 3.1669;
v_accuracy := greatest(v_accuracy, 0.0);
v_accuracy := least(v_accuracy, 100.0);
return(v_accuracy);
end calc_accuracy;
function calc_judgement (p_winpercent_before in double, p_winpercent_after in double) return varchar2
as
v_win_diff double;
v_judgement varchar2(100);
begin
if p_winpercent_after >= p_winpercent_before then
return ('ENGINE');
end if;
v_win_diff := p_winpercent_before - p_winpercent_after;
if v_win_diff >= 30.0 then
v_judgement := 'BLUNDER';
elsif v_win_diff >= 20.0 then
v_judgement := 'MISTAKE';
elsif v_win_diff >= 10.0 then
v_judgement := 'INACCURACY';
end if;
return(v_judgement);
end calc_judgement;
function calc_sharpness (p_win in integer, p_loose in integer) return double
as
v_win_rescaled double;
v_loose_rescaled double;
v_sharpness double;
begin
if p_win = 0 or p_loose = 0 then
return null;
end if;
v_win_rescaled := p_win / 1000.0;
v_loose_rescaled := p_loose / 1000.0;
v_sharpness := pow(2.0 / (log(1.0 / v_win_rescaled - 1.0) + log(1.0 / v_loose_rescaled - 1.0)), 2);
return v_sharpness;
end calc_sharpness;
procedure upsert_da_position(p_da_position_rec in da_position%rowtype)
as
begin
insert into da_position values (p_da_position_rec.position_id,
p_da_position_rec.white_winning_chances,
p_da_position_rec.white_score_rate,
p_da_position_rec.white_draw_rate,
p_da_position_rec.black_winning_chances,
p_da_position_rec.black_score_rate,
p_da_position_rec.black_draw_rate,
p_da_position_rec.accuracy,
p_da_position_rec.judgement,
p_da_position_rec.sharpness
)
on duplicate key
update white_winning_chances = p_da_position_rec.white_winning_chances,
white_score_rate = p_da_position_rec.white_score_rate,
white_draw_rate = p_da_position_rec.white_draw_rate,
black_winning_chances = p_da_position_rec.black_winning_chances,
black_score_rate = p_da_position_rec.black_score_rate,
black_draw_rate = p_da_position_rec.black_draw_rate,
accuracy = p_da_position_rec.accuracy,
judgement = p_da_position_rec.judgement,
sharpness = p_da_position_rec.sharpness;
end upsert_da_position;
PROCEDURE gen_da_position(p_player_id NUMBER(20))
as
v_total_prv, v_total, v_win_rate_prv, v_win_rate, v_white_winning_chances_prv, v_white_winning_chances, v_score double;
v_score_rate, v_draw_rate, v_loss_rate, v_white_score_rate, v_black_score_rate double;
v_loss_rate_prv, v_accuracy, v_black_winning_chances_prv, v_black_winning_chances double;
v_white_draw_rate, v_black_draw_rate double;
v_judgement varchar2(100);
v_da_position_rec da_position%rowtype;
begin
for v_rec in
(
select
lag(g.id) over (order by g.id, p.half_move_num) as game_id_prv,
g.id as game_id,
pa.position_id,
p.half_move_num,
decode(p.move_white, '', null, p.move_white) move_white,
decode(p.move_black, '', null, p.move_black) move_black,
lag(pa.best_move_uci) over (order by g.id, p.half_move_num) as best_move_uci_prv,
pa.best_move_uci,
lag(pa.centipawn) over (order by g.id, p.half_move_num) as centipawn_prv,
pa.centipawn,
lag(pa.wins) over (order by g.id, p.half_move_num) as wins_prv,
pa.wins,
lag(pa.draws) over (order by g.id, p.half_move_num) as draws_prv,
pa.draws,
lag(pa.losses) over (order by g.id, p.half_move_num) as losses_prv,
pa.losses
from
game g
join player pw on
g.white_player_id = pw.id
join player pb on
g.black_player_id = pb.id
join position p on
(g.id = p.game_id)
join position_analysis pa on
(p.id = pa.position_id)
where
pw.id = p_player_id
or pb.id = p_player_id
order by g.id, p.half_move_num
)
loop
if v_rec.best_move_uci_prv is null or v_rec.game_id <> v_rec.game_id_prv
then
continue; -- no move evaluation available
end if;
v_da_position_rec := null;
v_total_prv := v_rec.wins_prv + v_rec.draws_prv + v_rec.losses_prv;
v_win_rate_prv := v_rec.wins_prv / v_total_prv;
v_loss_rate_prv := v_rec.losses_prv / v_total_prv;
v_white_winning_chances_prv := calc_win_percent(v_rec.centipawn_prv);
v_black_winning_chances_prv := 100 - v_white_winning_chances_prv;
v_total := v_rec.wins + v_rec.draws + v_rec.losses;
v_score := v_rec.wins + v_rec.draws / 2;
v_score_rate := v_score / v_total;
v_win_rate := v_rec.wins / v_total;
v_draw_rate := v_rec.draws / v_total;
v_loss_rate := v_rec.losses / v_total;
v_white_winning_chances := calc_win_percent(v_rec.centipawn);
v_black_winning_chances := 100 - v_white_winning_chances;
-- logging.log('v_white_winning_chances: '||v_white_winning_chances);
-- logging.log('v_black_winning_chances: '||v_black_winning_chances);
if (v_rec.half_move_num MOD 2 = 0)
then -- black moved
v_black_score_rate := 100 * v_score_rate;
v_white_score_rate := 100 * (1 - v_score_rate);
if (v_rec.move_black = v_rec.best_move_uci_prv) then
v_accuracy := 100.0;
v_judgement := 'ENGINE';
else
v_accuracy := calc_accuracy(v_black_winning_chances_prv, v_black_winning_chances);
v_judgement := calc_judgement(v_black_winning_chances_prv, v_black_winning_chances);
end if;
else -- white moved
v_white_score_rate := 100 * v_score_rate;
v_black_score_rate := 100 * (1 - v_score_rate);
if (v_rec.move_white = v_rec.best_move_uci_prv) then
v_accuracy := 100.0;
v_judgement := 'ENGINE';
else
v_accuracy := calc_accuracy(v_white_winning_chances_prv, v_white_winning_chances);
v_judgement := calc_judgement(v_white_winning_chances_prv, v_white_winning_chances);
end if;
end if;
v_white_draw_rate := 100 * v_draw_rate;
v_black_draw_rate := 100 * v_draw_rate;
--
-- set record data
--
v_da_position_rec.position_id := v_rec.position_id;
v_da_position_rec.white_winning_chances := v_white_winning_chances;
v_da_position_rec.white_score_rate := v_white_score_rate;
v_da_position_rec.white_draw_rate := v_white_draw_rate;
v_da_position_rec.black_winning_chances := v_black_winning_chances;
v_da_position_rec.black_score_rate := v_black_score_rate;
v_da_position_rec.black_draw_rate := v_black_draw_rate;
v_da_position_rec.accuracy := v_accuracy;
v_da_position_rec.judgement := v_judgement;
v_da_position_rec.sharpness := calc_sharpness(v_rec.wins, v_rec.losses);
--
-- upsert record
--
upsert_da_position(v_da_position_rec);
end loop;
end gen_da_position;
procedure gen_da1game (p_game_id NUMBER(20))
as
v_acpl_white double;
v_acpl_black double;
v_stdcpl_white double;
v_stdcpl_black double;
v_accuracy_avg_white double;
v_accuracy_avg_black double;
v_sum_engine_moves_white integer;
v_sum_engine_moves_black integer;
v_sum_normal_moves_white integer;
v_sum_normal_moves_black integer;
v_sum_inaccurate_moves_white integer;
v_sum_inaccurate_moves_black integer;
v_sum_mistake_moves_white integer;
v_sum_mistake_moves_black integer;
v_sum_blunder_moves_white integer;
v_sum_blunder_moves_black integer;
v_game_length integer;
begin
select
avg(cpl_white) acpl_white,
avg(cpl_black) acpl_black,
stddev_samp(cpl_white) stdcpl_white,
stddev_samp(cpl_black) stdcpl_black,
avg(case when cpl_white is not null then accuracy else null end) accuracy_avg_white,
avg(case when cpl_black is not null then accuracy else null end) accuracy_avg_black,
sum(case when cpl_white is not null and judgement = 'ENGINE' then 1 else 0 end) sum_engine_moves_white,
sum(case when cpl_black is not null and judgement = 'ENGINE' then 1 else 0 end) sum_engine_moves_black,
sum(case when cpl_white is not null and judgement is null then 1 else 0 end) sum_normal_moves_white,
sum(case when cpl_black is not null and judgement is null then 1 else 0 end) sum_normal_moves_black,
sum(case when cpl_white is not null and judgement = 'INACCURACY' then 1 else 0 end) sum_inaccurate_moves_white,
sum(case when cpl_black is not null and judgement = 'INACCURACY' then 1 else 0 end) sum_inaccurate_moves_black,
sum(case when cpl_white is not null and judgement = 'MISTAKE' then 1 else 0 end) sum_mistake_moves_white,
sum(case when cpl_black is not null and judgement = 'MISTAKE' then 1 else 0 end) sum_mistake_moves_black,
sum(case when cpl_white is not null and judgement = 'BLUNDER' then 1 else 0 end) sum_blunder_moves_white,
sum(case when cpl_black is not null and judgement = 'BLUNDER' then 1 else 0 end) sum_blunder_moves_black,
max(half_move_num) game_length
into
v_acpl_white,
v_acpl_black,
v_stdcpl_white,
v_stdcpl_black,
v_accuracy_avg_white,
v_accuracy_avg_black,
v_sum_engine_moves_white,
v_sum_engine_moves_black ,
v_sum_normal_moves_white,
v_sum_normal_moves_black,
v_sum_inaccurate_moves_white,
v_sum_inaccurate_moves_black,
v_sum_mistake_moves_white,
v_sum_mistake_moves_black,
v_sum_blunder_moves_white,
v_sum_blunder_moves_black,
v_game_length
from
(
select
t.half_move_num ,
t.move_white,
t.move_black,
t.best_move_uci,
t.centipawn,
case
when t.half_move_num mod 2 = 0 then null
else case
when t.accuracy >= 99 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_white,
case
when t.half_move_num mod 2 = 1 then null
else case
when t.accuracy >= 99 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_black,
t.accuracy,
t.judgement ,
t.sharpness
from
(
select
p.half_move_num ,
case
when p.half_move_num mod 2 = 1 then 1
else -1
end inverse_sign,
p.move_white ,
p.move_black ,
pa.best_move_uci ,
pa.centipawn ,
lag(pa.centipawn) over (
order by
p.game_id,
p.half_move_num ) as centipawn_prv,
dp.accuracy,
dp.judgement ,
dp.sharpness
from
chess.position p
join chess.position_analysis as pa on
p.id = pa.position_id
left outer join chess.da_position as dp on
dp.position_id = pa.position_id
where
p.game_id = p_game_id
order by
p.game_id,
p.half_move_num ) t ) t2;
insert into
da_game (game_id,
acpl_white,
acpl_black,
stdcpl_white,
stdcpl_black,
accuracy_avg_white,
accuracy_avg_black,
sum_engine_moves_white,
sum_engine_moves_black,
sum_normal_moves_white,
sum_normal_moves_black,
sum_inaccurate_moves_white,
sum_inaccurate_moves_black,
sum_mistake_moves_white,
sum_mistake_moves_black,
sum_blunder_moves_white,
sum_blunder_moves_black,
game_length)
values (p_game_id,
v_acpl_white,
v_acpl_black,
v_stdcpl_white,
v_stdcpl_black,
v_accuracy_avg_white,
v_accuracy_avg_black,
v_sum_engine_moves_white,
v_sum_engine_moves_black,
v_sum_normal_moves_white,
v_sum_normal_moves_black,
v_sum_inaccurate_moves_white,
v_sum_inaccurate_moves_black,
v_sum_mistake_moves_white,
v_sum_mistake_moves_black,
v_sum_blunder_moves_white,
v_sum_blunder_moves_black,
v_game_length);
end gen_da1game;
procedure gen_da_game
as
begin
truncate table da_game;
for v_rec in (select distinct p.game_id from da_position dap join position p on p.id =dap.position_id order by game_id)
loop
gen_da1game(v_rec.game_id);
commit;
end loop;
end gen_da_game;
end da;
//
DELIMITER ;DA Package Spezifikation und Body
Neben internen Hilfsfunktionen zur Berechnung der abgeleiteten Kennzahlen und dem Speichern in der Datenbank enthält das Package da die Prozedur gen_da_position mit dem Parameter p_player, für welchen die entsprechenden Kennzahlen erzeugt werden. Eventuell bereits vorhandene Daten in der Tabelle da_position werden bei erneutem Aufruf der Prozedur überschrieben.
Generierung der abgeleiteten Kennzahlen
Um die abgeleiteten Kennzahlen für alle Partien eines bestimmten Spielers zu erzeugen, rufen wir die Package-Prozedur mit dem entsprechenden Wert der Spalte id aus der Tabelle player auf. Wie unten gezeigt führen wir die Datenbank-Prozedur im Rahmen eines PL/SQL-Blocks für jede einzelne Spieler-ID separat aus und schreiben die Transaktion am Ende mit commit fest (der konkrete ID-Wert ist natürlich Datenbank-spezifisch). Die Ausführungszeit dafür beträgt weniger als eine Minute.
Evaluation
Wir prüfen unsere Ergebnisse wieder anhand eines prominenten Beispiels aus der Schachgeschichte, hier Runde 11 aus dem Weltmeisterschaftskampf zwischen Emanuel Lasker und José Raoul Capablanca von 1921. Diese Partie wurde in der Vergangenheit ausführlich analysiert und auch auf Youtube vorgeführt.
Mit den zugehörigen ID-Werten für Spieler und Partie ist die SQL-Anweisung zur Datenermittlung rasch formuliert.
set @player_id=4364570 ; # Lasker
set @game_id=3692615 ; # World Championship 12th
select
pw.name,
pb.name,
p.half_move_num ,
p.move_white ,
p.move_black ,
pa.best_move_uci ,
pa.centipawn ,
pa.wins ,
pa.draws ,
pa.losses,
da.white_winning_chances,
da.white_score_rate,
da.white_draw_rate,
da.black_winning_chances,
da.black_score_rate,
da.black_draw_rate,
da.accuracy,
da.judgement,
da.sharpness
from
game g
join player pw on
g.white_player_id = pw.id
join player pb on
g.black_player_id = pb.id
join position p on
(g.id = p.game_id)
left outer join position_analysis pa on
(p.id = pa.position_id)
left outer join da_position da on
(da.position_id = pa.position_id )
where
(pw.id = @player_id
or pb.id = @player_id)
and g.id = @game_id
order by
p.half_move_num;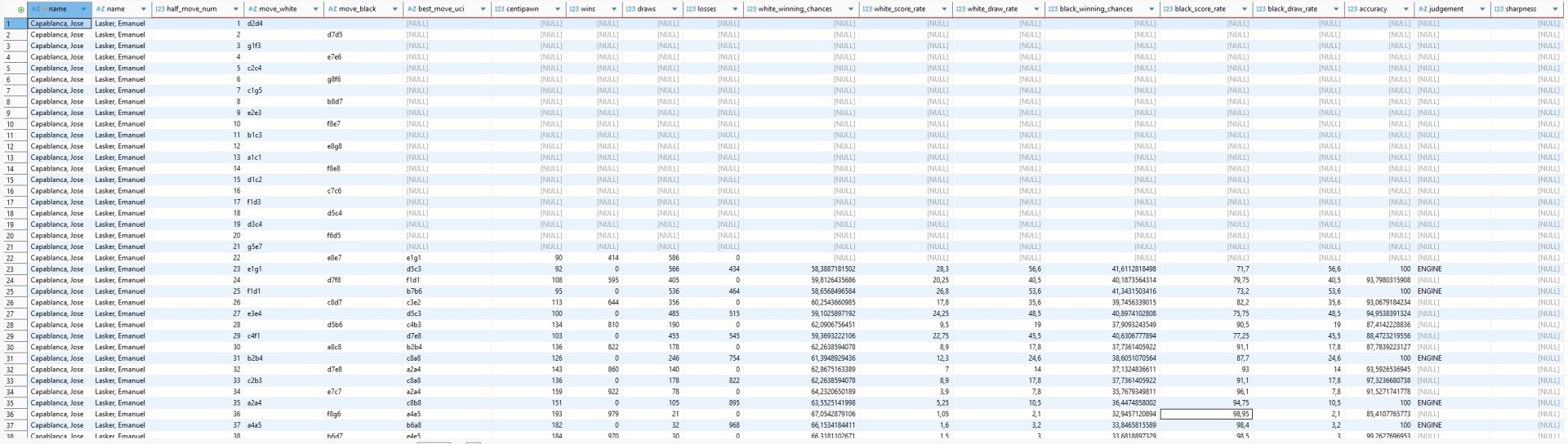
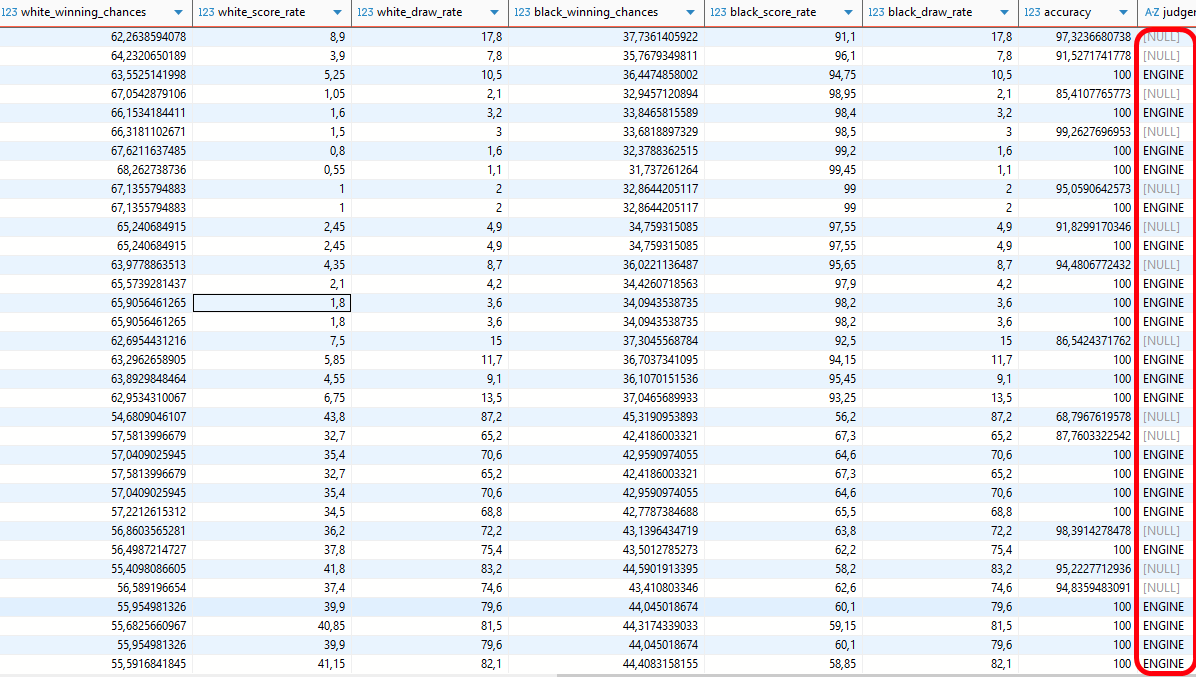
Wir sehen im obigen Bild (hier klicken zur besseren Ansicht) mittig die bereits bekannten Stockfish-Kennzahlen (best_move_uci, centipawn, wins, draws, losses) sowie rechts davon (ab Spalte white_winning_chances) die daraus abgeleiteten Kennzahlen. Da alle Stellungen vor dem 22. Halbzug vor dieser Partie historisch bekannt waren, wurde die Kennzahlenberechnung hierfür unterdrückt.
Sehen wir uns einige Schlüsselstellungen dieser Partie an (vgl. obige Analyse).
Der erste interessante Zug der Partie ist 11) …Te8-e7, der allgemein als Fehler eingestuft wird. Da aber alle Züge bis dahin bekannt waren, liegt uns kein Zugvorschlag der engine für die Ausgangsstellung nach Halbzug 21 vor. Und wenn wir den Wert des besten Zuges an dieser Stelle nicht kennen, können wir nicht wissen, wie weit wir mit dem Partiezug daneben liegen. Es bedeutet im Klartext, dass zur jeweils ersten analysierten Position jeder Schachpartie keine abgeleiteten Kennzahlen existieren, weil diese konstruktionsbedingt auch von der (nicht analysierten) Ausgangsstellung abhängen.
Das ist beispielsweise an dieser konkreten Stelle zwar bedauerlich, aber prinzipiell unvermeidlich.
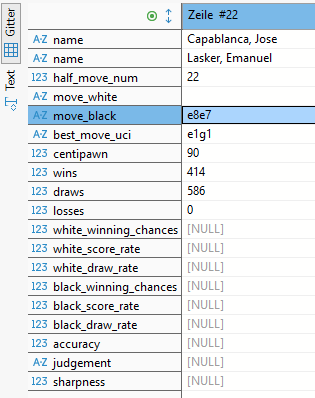
Auf der anderen Seite muss die Frage gestellt werden, wieso der damalige amtierenden Weltmeister diesen Zug spielte, wenn ihm die Stellung hätte bekannt sein müssen. Schlimmer noch, ein Jahr zuvor hatte Lasker exakt diese Position selbst auf dem Brett, wenn auch mit vertauschten Farben. Auch sein Herausforderer Capablanca hatte bereits 1916 den besseren Zug 11) …Dd8-e7 gespielt. War Lasker einfach nur schlecht vorbereitet in den Wettkampf gezogen?
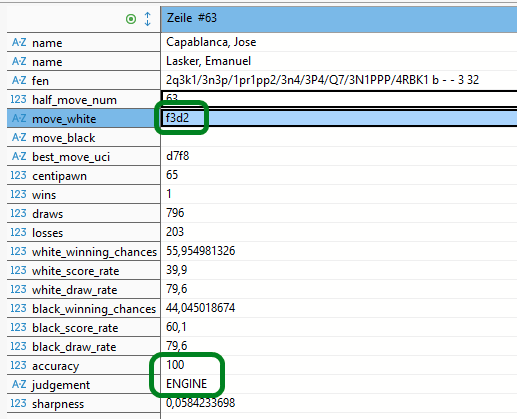
In der Folge dieser Partie fällt auf, dass vornehmlich der Herausforderer sehr viele „ENGINE-Züge“ spielt, was auf eine gute Strategie hinweist.
Insbesondere der sehr starke Abgabe-Zug 32) Lf3-d2 wird von Stockfish gebührend gewürdigt.
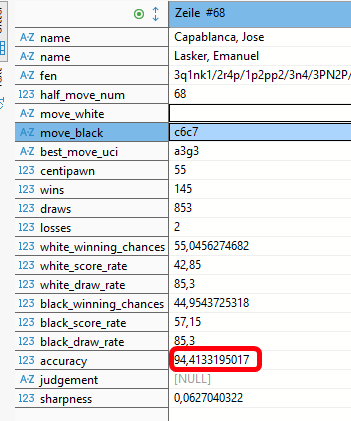
Der nächste interessante Zug ist 34)…Tc6-c7
Capablanca hält diesen für den eigentlichen Verlustzug, vermutlich aufgrund seines strategischen Denkens, das der Vertreibung des weissen Springers vom Feld e4 den Vorzug gibt.
Stockfish ist hier anderer Ansicht und straft Tc7 nur mit einem minimalen Abzug von der Bestnote.
Es ist vielmehr drei Züge später 37)…Ta7-a5, was die schwarze Stellung dramatisch verschlechtert und rasch zu deren Niedergang führt.
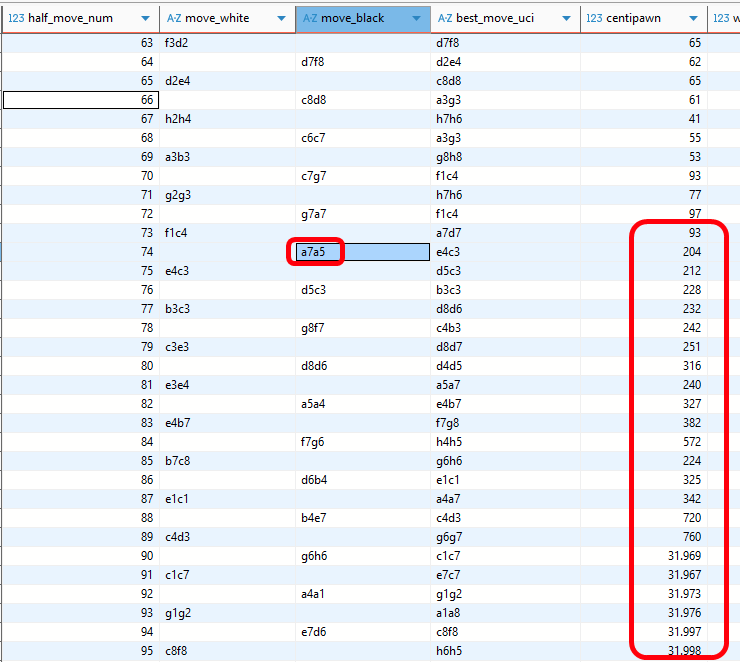
Interessanterweise wurde dieser Zug von den menschlichen Analysten und Kommentatoren weder explizit bemängelt, noch die bessere Fortsetzung 37)…Ta7-d7 vorgeschlagen.
Jedenfalls ermutigt uns das bisher erzielte Ergebnis zur Schaffung weiter Kennzahlen auf Partie-Ebene, der wir uns im nächsten Kapitel widmen werden…



Pingback: 10) die Analyse – Umfang und Laufzeiten
Pingback: 12) Spiel-Statistik