Im vorherigen Kapitel hatten wir abgeleitete Kennzahlen auf der Ebene von einzelnen Schach-Positionen und Zügen definiert, diese berechnet und in der Datenbank-Tabelle da_position gespeichert.
ACPL
Darauf aufbauend werden wir nun wie angekündigt weitere Statistiken erstellen, immer bezogen auf eine ganze Schachpartie, und beginnen dabei mit dem ACPL-Wert, welcher die durchschnittliche Abweichung in Centipawn-Einheiten vom jeweils besten Zug berechnet. Kleine ACPL-Werte legen nahe, dass vorwiegend gute Züge nahe am Optimum von der entsprechenden Seite gespielt wurden.
Wir werden die ACPL-Werte für beide Seiten berechnen, da wir auch daran interessiert sind, wie gut die Gegenspieler in den betreffenden Partien agierten.
Betrachten wir dazu eine zufällige Partie aus unserem Fundus, indem wir die einzelnen Positionen/Züge mit den zugehörigen Kennzahlen in unserer Datenbank verknüpfen. Dazu berechnen wir gleich noch die Differenz zwischen der Centipawn-Bewertung für den besten Zug (aus der vorherigen Zeile) und dem Centipawn-Wert für den real ausgeführten Zug.
select
t.fen, t.half_move_num , t.move_white, t.move_black, t.best_move_uci, t.centipawn, t.centipawn_prv, (t.centipawn_prv - t.centipawn) cp_diff, t.accuracy
from
(
select
p.fen,
p.half_move_num ,
p.move_white ,
p.move_black ,
pa.best_move_uci ,
pa.centipawn ,
lag(pa.centipawn) over (
order by p.game_id,
p.half_move_num ) as centipawn_prv,
dp.accuracy
from
chess.position p
join chess.position_analysis as pa on
p.id = pa.position_id
left outer join chess.da_position as dp on
dp.position_id = pa.position_id
where
p.game_id = 2124959
order by
p.game_id,
p.half_move_num ) t;In der Spalte „cp_diff“ unten im Bild finden sich die Ausgangswerte zur Berechnung der ACPL-Kennzahlen.
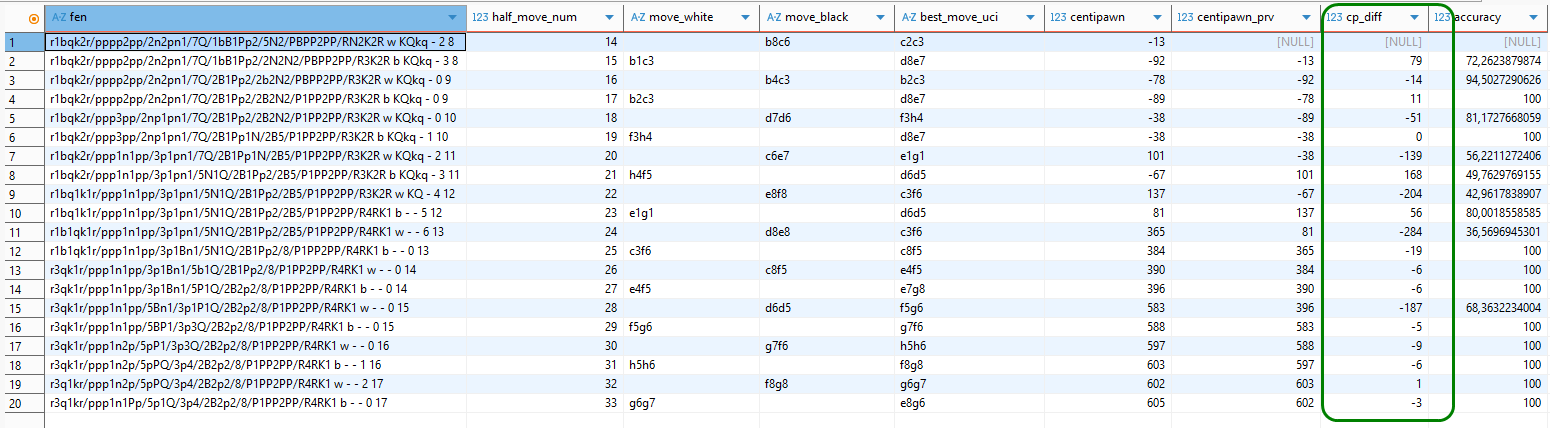
Im Bild oben haben wir der Übersichtlichkeit halber der centipawn-Bewertung der betreffenden Zeile bzw. Schachposition (in Spalte fen) die Centipawn-Bewertung der Ausgangsposition (aus der Zeile darüber) beigeordnet (Spalte centipawn_prv). Die Werte in der Spalte cp_diff ergeben sich nun einfach aus der Differenz centipawn_prv – centipawn.
Sehen wir uns die Werte von cp_diff genauer an. Zunächst stellen wir fest, dass in der allerersten Zeile der Wert dafür fehlt. Die Ursache liegt auf der Hand – für die erste Zeile fehlt der Vorgängerwert und damit die Berechnungsgrundlage. Das ist ok.
In der zweiten Zeile zog Weiß den suboptimalen Zug Sb1-c3, wodurch die centipawn-Bewertung von -13 (also einem marginalen Vorteil von Schwarz) auf -92 (fast einen ganzen Bauern) absackte. Dies manifestiert sich absolut in einem Verlustwert von 79 centipawn in der cp_diff-Spalte und lässt sich gleichfalls am accuracy-Wert von nur ca. 72% ablesen. Auch dieses Ergebnis erscheint plausibel.
In der dritten Zeile zog Schwarz Lb4-c3, statt des empfohlenen Dd8-e7, woraus sich eine Differenz von -14 ergibt. Dass hier eine negative Zahl entsteht, erscheint auf den ersten Blick widersinnig, da wir sie ja als Verlust in Hinblick auf den optimalen centipawn-Wert interpretieren wollen. Dabei zu berücksichtigen ist allerdings, dass die centipawn-Bewertung bewusst aus der Sicht von Weiß definiert wurde. Ein negativer Verlust bedeutet daher einen Gewinn für Weiß und das wiederum einen Wertverlust für Schwarz.
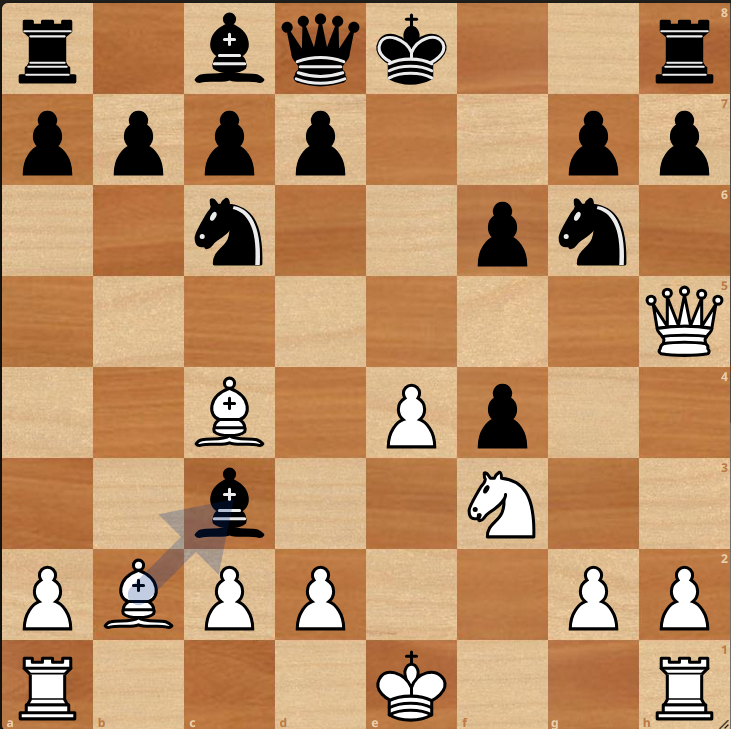
Wir berechnen daher eine Kennzahl cpl („centipawn loss“) aus dem Differenzwert, indem wir zusätzlich das Vorzeichen umkehren, falls Schwarz am Zug war. Warum wir stattdessen nicht einfach den Absolutwert heranziehen, sehen wir gleich.
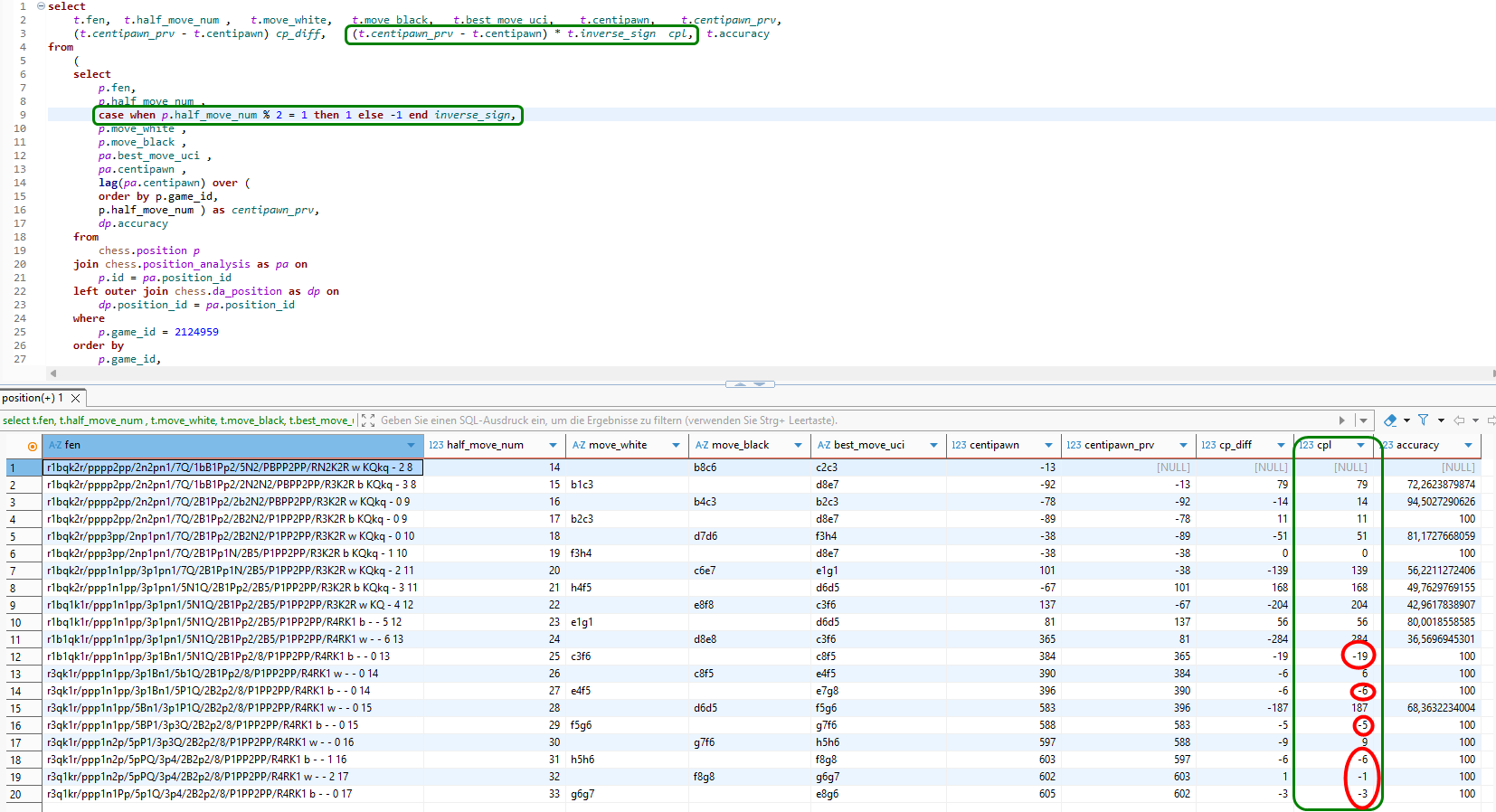
Wir hätten nun erwartet, dass die Verlustwerte in der neuen Spalte cpl alle positiv oder 0 (im Falle von 100% accuracy) sind. Doch wie kann es sein, dass in der Spalte cpl Werte ungleich 0 auch dann auftauchen, wenn der vorgeschlagene optimale Schachzug tatsächlich ausgeführt wurde?!
Betrachten wir zum Beispiel gleich die vierte Zeile. Es wurde genau der vorgeschlagene Zug 9) Lb2-c3 ausgeführt und trotzdem entstand ein centipawn-Verlust von 11!
Nun, das ist zu erklären. In der Position nach 9) Lb2-c3 kann Stockfish erstens auf die vorherige Analyse aufbauen und zweitens diese nun um mindestens einen Halbzug vertiefen. Dadurch kann es zu einem abweichenden Resultat bei der Bewertung kommen. Und solange das Schachprogramm keine zwingende Variante zur Mattsetzung gefunden hat, sind alle Bewertungsergebnisse stets mit dem Makel der Unvollkommenheit behaftet!
Wie wollen wir also mit dieser Situation umgehen? Wenn wir den cpl-Wert nun umdefinieren, dass auch negative Verluste möglich wären, würde das bedeuten, dass wir Züge besser als den „optimalen“ Zug einstufen müssten. Das passte dann nicht mehr zur accuracy oder man müsste dafür Werte größer als 100% zulassen und neu berechnen.
Dadurch entstünde eine kaum noch zu durchschauende Komplexität und Intransparenz, so dass wir lieber die näherliegende und leicht verständliche Herangehensweise vorziehen, den cpl-Wert immer dann auf 0 zu setzen, wenn die accuracy 100% beträgt.
Bevor wir dies umsetzen, müssen wir eine weitere Anomalie beheben. Angenommen, Weiß kann seinen Gegner in 5 Zügen matt setzen. Definitionsgemäß haben wir die centipawn-Bewertung in dieser Situation auf den exorbitant hohen Wert 32000 gesetzt. Wenn nun Weiß stattdessen einen anderen Zug wählt, der immer noch zu einer total gewonnenen Position für ihn führt mit z.B. einer centipawn-Bewertung von 2000, dann wäre der cpl-Wert für diesen Zug 30000, was sich auf den Durchschnittswert ACPL verheerend auswirken würde. Damit wir diese fatalen Ausschläge erkennen und beheben können, betrachten wir bei der cpl-Berechnung zusätzlich die Kennzahl accuracy.
Liegt diese bei 99% oder höher, setzen wir den cpl-Wert standardmäßig auf 0.
In diesem Zusammenhang trennen wir den cpl-Wert gleich noch auf in cpl_white und cpl_black und passen unsere SQL-Abfrage entsprechend an.
select
t.fen,
t.half_move_num ,
t.move_white,
t.move_black,
t.best_move_uci,
t.centipawn,
case
when t.half_move_num % 2 = 0 then null
else case
when t.accuracy >= 99 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_white,
case
when t.half_move_num % 2 = 1 then null
else case
when t.accuracy >= 99 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_black,
t.accuracy
from
(
select
p.fen,
p.half_move_num ,
case
when p.half_move_num % 2 = 1 then 1
else -1
end inverse_sign,
p.move_white ,
p.move_black ,
pa.best_move_uci ,
pa.centipawn ,
lag(pa.centipawn) over (
order by
p.game_id,
p.half_move_num ) as centipawn_prv,
dp.accuracy
from
chess.position p
join chess.position_analysis as pa on
p.id = pa.position_id
left outer join chess.da_position as dp on
dp.position_id = pa.position_id
where
p.game_id = 2124959
order by
p.game_id,
p.half_move_num ) t;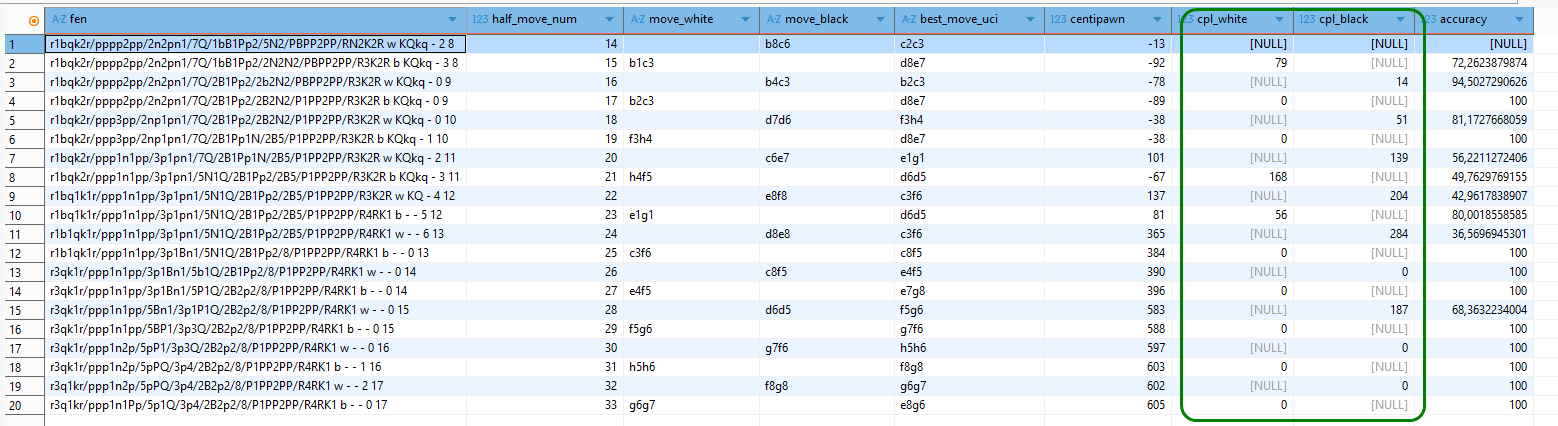
STDCPL
ACPL („average centipawn loss“) ist wie der Name bereits ausdrückt ein Durchschnittswert. Dabei ist ein möglichst niedriger Wert zwar gut, aber allein nicht unbedingt aussagekräftig. Denn die beste Gegenwehr nutzt einem Spieler wenig, wenn er z.B. einmal einen Verlustzug ausgeführt hat, den der Gegenspieler auszunutzen versteht. Selbst wenn der Spieler von dort an jeden Zug mit einer Genauigkeit von 100% spielt, muss er die Partie verlieren. Um diesen Sachverhalt sichtbar zu machen, benutzen wir die Standardabweichung der cpl-Werte als statistisches Maß hierfür. Je kleiner dieser Wert ist, desto geringer ist die Wahrscheinlichkeit für einen groben Schnitzer.
Für die Berechnung von ACPL und der neuen Kennzahl STDCPL ( „Standard Deviation Centipawn Loss“) benutzen wir die eingebauten Funktionen AVG() und STDDEV_SAMP() von MariaDB.
select
avg(cpl_white) acpl_white,
avg(cpl_black) acpl_black,
stddev_samp(cpl_white) stdcpl_white,
stddev_samp(cpl_black) stdcpl_black,
avg(case when cpl_white is not null then accuracy else null end) accuracy_avg_white,
avg(case when cpl_black is not null then accuracy else null end) accuracy_avg_black
from
(
select
t.fen,
t.half_move_num ,
t.move_white,
t.move_black,
t.best_move_uci,
t.centipawn,
case
when t.half_move_num % 2 = 0 then null
else case
when t.accuracy = 100 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_white,
case
when t.half_move_num % 2 = 1 then null
else case
when t.accuracy = 100 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_black,
t.accuracy
from
(
select
p.fen,
p.half_move_num ,
case
when p.half_move_num % 2 = 1 then 1
else -1
end inverse_sign,
p.move_white ,
p.move_black ,
pa.best_move_uci ,
pa.centipawn ,
lag(pa.centipawn) over (
order by
p.game_id,
p.half_move_num ) as centipawn_prv,
dp.accuracy
from
chess.position p
join chess.position_analysis as pa on
p.id = pa.position_id
left outer join chess.da_position as dp on
dp.position_id = pa.position_id
where
p.game_id = 2124959
order by
p.game_id,
p.half_move_num ) t ) t2;Im obigen Match „Goliath vs David“ entsprechen die resultierenden ACPL– und STDCPL-Werte voll und ganz unseren Erwartungen.

Wenn wir die Korrektheit unserer Berechnungen für obige Partie überprüfen wollen, indem wir sie z.B. von lichess.org analysieren lassen, erhalten wir allerdings abweichende Ergebnisse, die sich nicht durch Rechenungenauigkeiten erklären lassen.
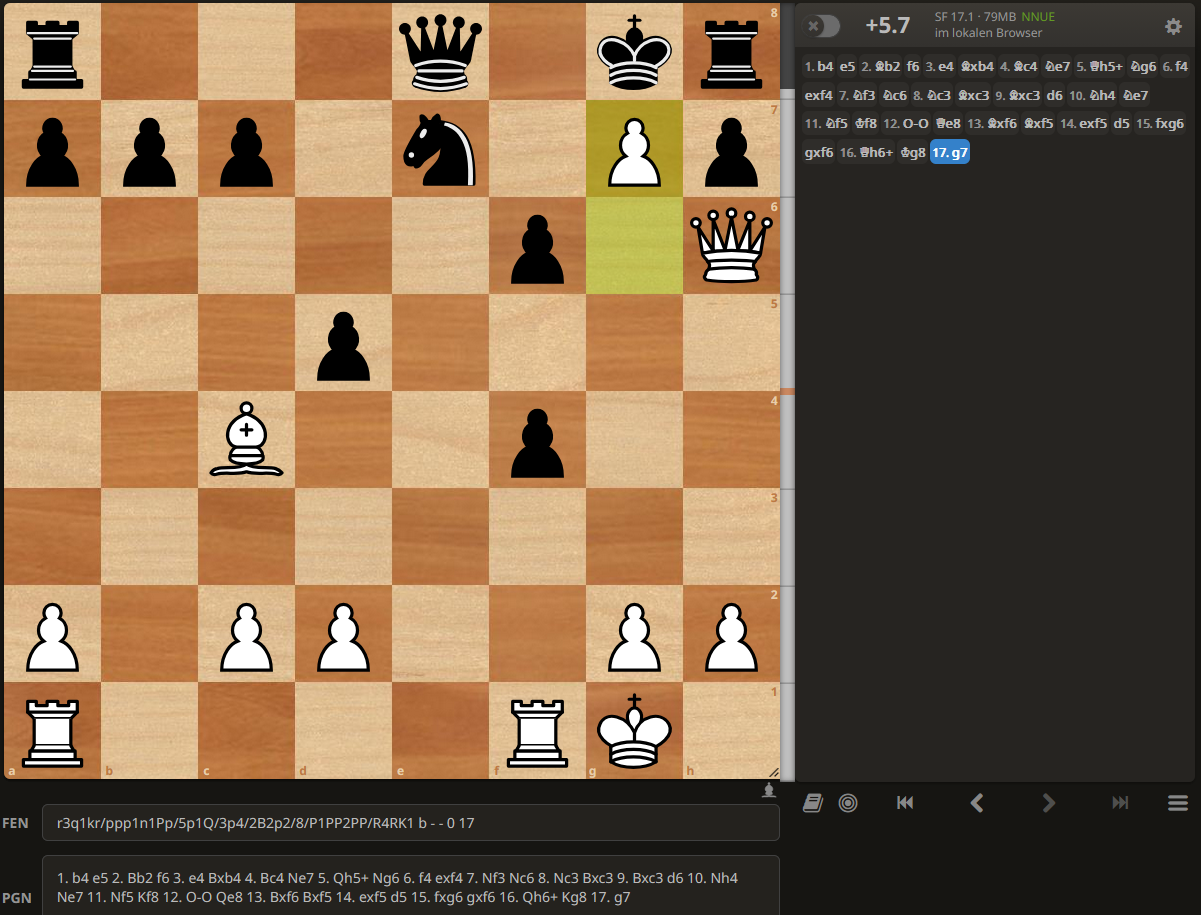
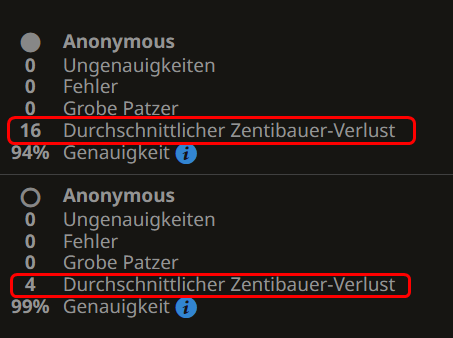
Haben wir also falsch gerechnet? Kurze Antwort: Nein, aber wir verwenden eine andere Berechnungsgrundlage.
Wenn wir uns nochmal die obigen Daten ansehen, machen wir uns wieder klar, dass wir die bekannten Eröffnungszüge aus den Theoriebüchern bewusst gar nicht bewerten wollten!
Dieser doch gravierende Unterschied zwischen den ACPL-Werten von lichess.org und unseren (4 vs 30 bzw. 16 vs 97) kennzeichnet den überragenden Einfluss von Eröffnungswissen im moderen Schachspiel. Doch was uns im Spielervergleich wirklich interessiert, ist Schachkönnen ohne Zuhilfenahme von dicken Eröffnungstheoriebüchern und vorbereiteten Varianten, evtl. ermittelt durch lange Computer-Analysen!
ACCURACY
Es steht zu vermuten, dass auch die Genauigkeitsrate sinken wird, wenn wir bekannte Eröffnungszüge unberücksichtigt lassen. Wir rechnen das kurz nach, indem wir unser SQL etwas erweitern.
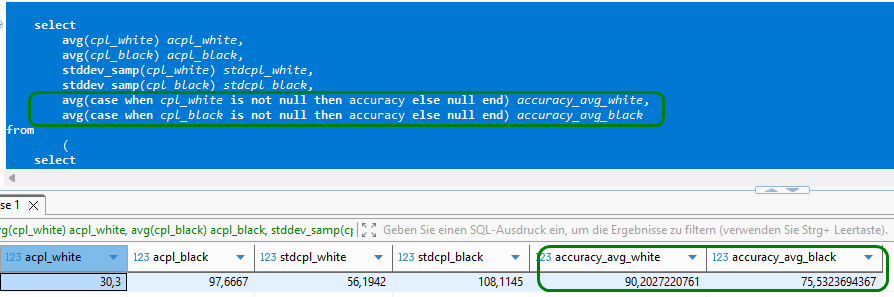
Wie fast nicht anders zu erwarten, sinken die Genauigkeits-Werte signifikant im Vergleich zur vollständigen Partie inklusive aller Züge aus dem Eröffnungsbuch.
Eine Anomalie
Folgende Situation vergleichbar zu dem obigen Fall ist denkbar: die Schachengine schlägt einen Zug vor mit einem errechneten centipawn-Wert x. Der Zugführende spielt aber einen alternativen Zug und die daraus resultierende Stellung wird mit einem centipawn-Wert y belohnt, wobei x < y !
Demnach korrigiert die engine nachträglich ihren eigenen Vorschlag. Tatsächlich finden wir in unseren Analysedaten Tausende solcher Fälle. Doch glücklicherweise werden auch diese Züge stets mit einer accuracy von 100% belohnt!
Stellungs-Komplexität
Wir hatten im vorigen Kapitel ein relativ aufwändiges Verfahren zur Beurteilung der Stellungskomplexität kurz vorgestellt und wegen dieses Aufwandes auch gleich wieder verworfen.
Wünschenswert wäre daher ein einfacher Indikator, mit dessen Hilfe wir beurteilen könnten, ob eine vorliegende Position kompliziert ist, wo spielbare Züge schwerer zu finden sind als in einer Position, wo der nächste Zug auf der Hand liegt bzw. sogar erzwungen ist. Dann ließe sich die Qualität von einzelnen Zügen gewichten, indem man gute Züge in einer schwierigen/einfachenPosition mit einem Bonus bzw. Malus versieht. Andersherum ließen sich schlechte Züge in schwierigen Positionen leichter verzeihen als in einfachen Positionen.
Eine naheliegender Kandidat für einen solchen Komplexitäts-Indikator wäre der Rechenaufwand, welchen Stockfish für die Stellungsanalyse erbringt. Dazu haben wir bereits die Kennzahlen nodes, depth, seldepth und time_sec für jeden Zug in der Tabelle position_analysis mitgeführt.
Zu diesem Zweck haben wir mit nodes etwas experimentiert, indem wir mit Hilfe von Erwartungswert und Standardabweichung die drei Klassen (-1, 0, 1 für „leicht“, „normal“ und „schwierig“) bildeten und einige bekannte Schachpartien daraufhin untersuchten.
select t3.half_move_num,
t3.move_white ,t3.move_black ,
t3.nodes_white,
#t3.avg_nodes_white ,
#t3.stdev_nodes_white ,
case when t3.nodes_white > t3.avg_nodes_white + t3.stdev_nodes_white then 1
when t3.nodes_white < t3.avg_nodes_white - t3.stdev_nodes_white then -1
else 0
end complexity_white,
t3.nodes_black,
#t3.avg_nodes_black,
#t3.stdev_nodes_black,
case when t3.nodes_black > t3.avg_nodes_black + t3.stdev_nodes_black then 1
when t3.nodes_black < t3.avg_nodes_black - t3.stdev_nodes_black then -1
else 0
end complexity_black
from (
select
t2.half_move_num,
t2.move_white ,t2.move_black ,
t2.nodes_white,
avg(t2.nodes_white) over () as avg_nodes_white ,
stddev_samp(t2.nodes_white) over () as stdev_nodes_white ,
t2.nodes_black,
avg(t2.nodes_black) over () as avg_nodes_black,
stddev_samp(t2.nodes_black) over () as stdev_nodes_black
from
(
select
t.half_move_num ,
t.move_white ,t.move_black ,
case
when t.half_move_num % 2 = 1 and t.accuracy is not null then t.nodes
else null
end nodes_white,
case
when t.half_move_num % 2 = 0 and t.accuracy is not null then t.nodes
else null
end nodes_black
from
(
select
p.half_move_num ,
p.move_white ,p.move_black ,
pa.nodes,
dp.accuracy
from
chess.position p
join chess.position_analysis as pa on
p.id = pa.position_id
left outer join chess.da_position as dp on
dp.position_id = pa.position_id
where
p.game_id = 10823787 # Schach-WM 1972: Partie 13, Spasski - Fischer
) t)t2)t3
order by
t3.half_move_num;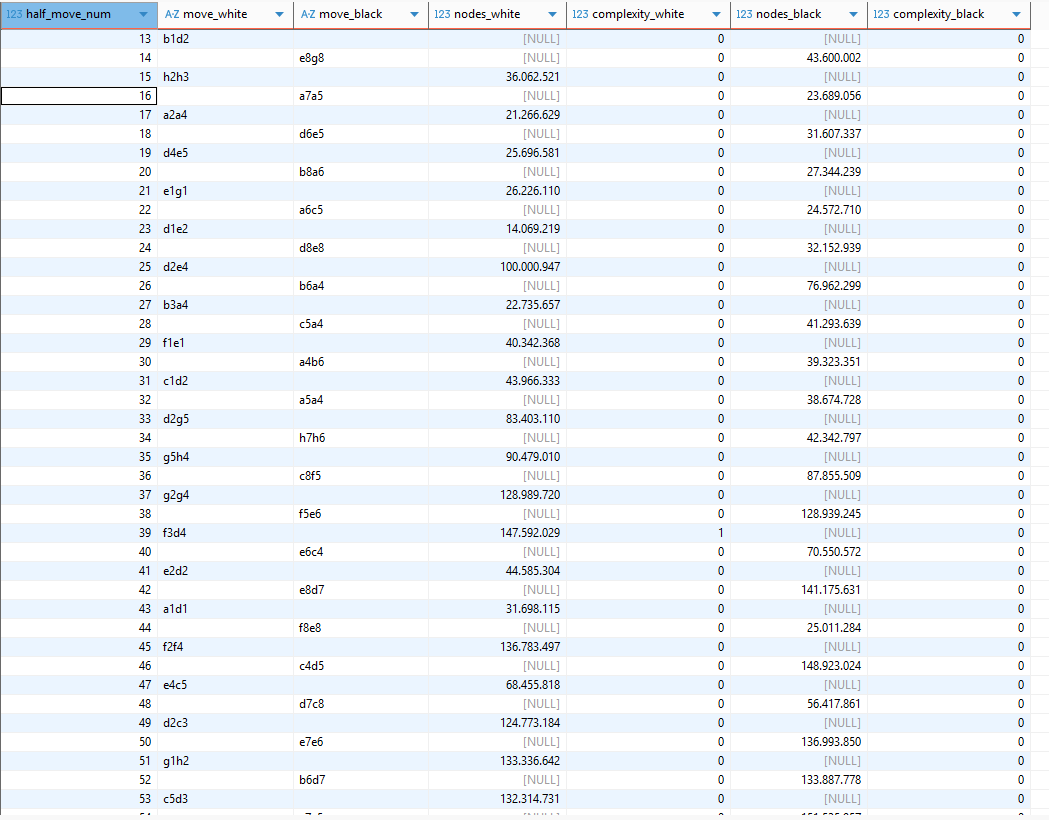
Nach eingehender Prüfung des Ergebnisses müssen wir allerdings feststellen, dass kein signifikanter Zusammenhang zwischen Rechenaufwand (in nodes) und tatsächlicher Stellungskomplexität erkennbar ist. Somit verwerfen wir diesen Ansatz wieder.
Sharpness
Wie bereits ausgeführt, lässt sich anhand der WDL-Bewertung von Stockfish diese Kennzahl schwerlich ablesen, so dass wir vorerst von einer weiteren Verdichtung auf Partieebene absehen.
weitere Aggregationen
Abschließend zählen wir für jede Partie die Anzahl Halbzüge sowie diejenigen Züge von Weiß und Schwarz, die wir als ‚BLUNDER‘, ‚MISTAKE‘, ‚ENGINE‘ und ‚NORMAL‘ (für die übrigen Züge) eingestuft hatten. Wir begnügen uns vorerst mit diesen Partie-Kennzahlen und starten mit der Implementierung.
Datenmodell-Erweiterung
Wie bereits skizziert, erstellen wir für die Partie-Kennzahlen eine separate Tabelle da_game, die wir mit der Tabelle game über eine entsprechende Fremdschlüssel-Beziehung verknüpfen.
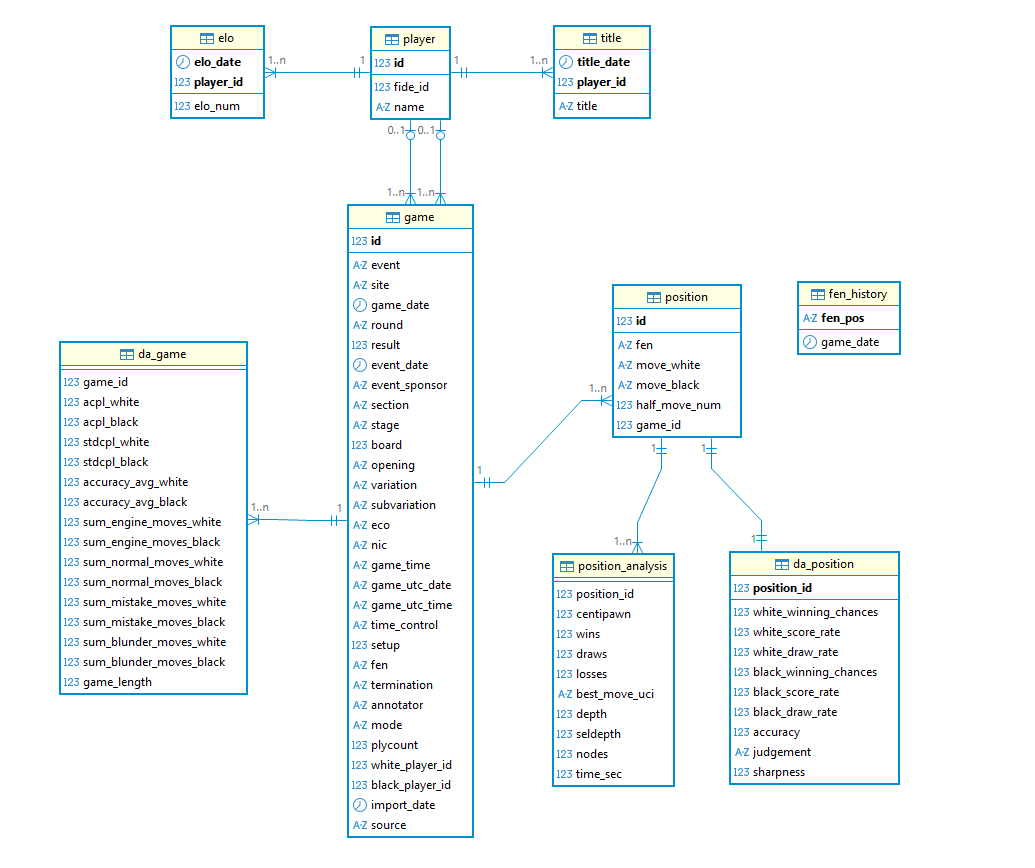
Package-Erweiterung
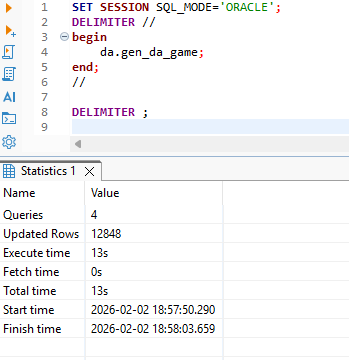
Zum Befüllen unserer neuen Tabelle erweitern wir das vorhandene PL/SQL-Package in der Datenbank. Die neue Prozedur gen_da_game löscht zunächst die Zieltabelle und iteriert danach über alle analysierten Partien, um für jede einzelne einen entsprechenden Datensatz in der Tabelle da_game einzutragen.
SET SESSION SQL_MODE='ORACLE';
DELIMITER //
CREATE OR REPLACE PACKAGE da AS
-- must be declared as public!
PROCEDURE gen_da_position(p_player_id NUMBER(20));
procedure gen_da_game;
END da;
//
CREATE OR REPLACE PACKAGE BODY da as
function calc_win_percent(p_centipawns in double) return double
as
v_win_percent double;
begin
v_win_percent := 50.0 + 50.0 * (2.0 / (1.0 + exp(-0.00368208 * p_centipawns)) - 1.0);
return v_win_percent;
end calc_win_percent;
function calc_accuracy (p_winpercent_before in double, p_winpercent_after in double) return double
as
v_win_diff double;
v_accuracy double;
begin
if p_winpercent_after >= p_winpercent_before then
return (100.0);
end if;
v_win_diff := p_winpercent_before - p_winpercent_after;
v_accuracy := 103.1668 * exp(-0.04354 * (v_win_diff)) - 3.1669;
v_accuracy := greatest(v_accuracy, 0.0);
v_accuracy := least(v_accuracy, 100.0);
return(v_accuracy);
end calc_accuracy;
function calc_judgement (p_winpercent_before in double, p_winpercent_after in double) return varchar2
as
v_win_diff double;
v_judgement varchar2(100);
begin
if p_winpercent_after >= p_winpercent_before then
return ('ENGINE');
end if;
v_win_diff := p_winpercent_before - p_winpercent_after;
if v_win_diff >= 30.0 then
v_judgement := 'BLUNDER';
elsif v_win_diff >= 20.0 then
v_judgement := 'MISTAKE';
elsif v_win_diff >= 10.0 then
v_judgement := 'INACCURACY';
end if;
return(v_judgement);
end calc_judgement;
function calc_sharpness (p_win in integer, p_loose in integer) return double
as
v_win_rescaled double;
v_loose_rescaled double;
v_sharpness double;
begin
if p_win = 0 or p_loose = 0 then
return null;
end if;
v_win_rescaled := p_win / 1000.0;
v_loose_rescaled := p_loose / 1000.0;
v_sharpness := pow(2.0 / (log(1.0 / v_win_rescaled - 1.0) + log(1.0 / v_loose_rescaled - 1.0)), 2);
return v_sharpness;
end calc_sharpness;
procedure upsert_da_position(p_da_position_rec in da_position%rowtype)
as
begin
insert into da_position values (p_da_position_rec.position_id,
p_da_position_rec.white_winning_chances,
p_da_position_rec.white_score_rate,
p_da_position_rec.white_draw_rate,
p_da_position_rec.black_winning_chances,
p_da_position_rec.black_score_rate,
p_da_position_rec.black_draw_rate,
p_da_position_rec.accuracy,
p_da_position_rec.judgement,
p_da_position_rec.sharpness
)
on duplicate key
update white_winning_chances = p_da_position_rec.white_winning_chances,
white_score_rate = p_da_position_rec.white_score_rate,
white_draw_rate = p_da_position_rec.white_draw_rate,
black_winning_chances = p_da_position_rec.black_winning_chances,
black_score_rate = p_da_position_rec.black_score_rate,
black_draw_rate = p_da_position_rec.black_draw_rate,
accuracy = p_da_position_rec.accuracy,
judgement = p_da_position_rec.judgement,
sharpness = p_da_position_rec.sharpness;
end upsert_da_position;
PROCEDURE gen_da_position(p_player_id NUMBER(20))
as
v_total_prv, v_total, v_win_rate_prv, v_win_rate, v_white_winning_chances_prv, v_white_winning_chances, v_score double;
v_score_rate, v_draw_rate, v_loss_rate, v_white_score_rate, v_black_score_rate double;
v_loss_rate_prv, v_accuracy, v_black_winning_chances_prv, v_black_winning_chances double;
v_white_draw_rate, v_black_draw_rate double;
v_judgement varchar2(100);
v_da_position_rec da_position%rowtype;
begin
for v_rec in
(
select
lag(g.id) over (order by g.id, p.half_move_num) as game_id_prv,
g.id as game_id,
pa.position_id,
p.half_move_num,
decode(p.move_white, '', null, p.move_white) move_white,
decode(p.move_black, '', null, p.move_black) move_black,
lag(pa.best_move_uci) over (order by g.id, p.half_move_num) as best_move_uci_prv,
pa.best_move_uci,
lag(pa.centipawn) over (order by g.id, p.half_move_num) as centipawn_prv,
pa.centipawn,
lag(pa.wins) over (order by g.id, p.half_move_num) as wins_prv,
pa.wins,
lag(pa.draws) over (order by g.id, p.half_move_num) as draws_prv,
pa.draws,
lag(pa.losses) over (order by g.id, p.half_move_num) as losses_prv,
pa.losses
from
game g
join player pw on
g.white_player_id = pw.id
join player pb on
g.black_player_id = pb.id
join position p on
(g.id = p.game_id)
join position_analysis pa on
(p.id = pa.position_id)
where
pw.id = p_player_id
or pb.id = p_player_id
order by g.id, p.half_move_num
)
loop
if v_rec.best_move_uci_prv is null or v_rec.game_id <> v_rec.game_id_prv
then
continue; -- no move evaluation available
end if;
v_da_position_rec := null;
v_total_prv := v_rec.wins_prv + v_rec.draws_prv + v_rec.losses_prv;
v_win_rate_prv := v_rec.wins_prv / v_total_prv;
v_loss_rate_prv := v_rec.losses_prv / v_total_prv;
v_white_winning_chances_prv := calc_win_percent(v_rec.centipawn_prv);
v_black_winning_chances_prv := 100 - v_white_winning_chances_prv;
v_total := v_rec.wins + v_rec.draws + v_rec.losses;
v_score := v_rec.wins + v_rec.draws / 2;
v_score_rate := v_score / v_total;
v_win_rate := v_rec.wins / v_total;
v_draw_rate := v_rec.draws / v_total;
v_loss_rate := v_rec.losses / v_total;
v_white_winning_chances := calc_win_percent(v_rec.centipawn);
v_black_winning_chances := 100 - v_white_winning_chances;
-- logging.log('v_white_winning_chances: '||v_white_winning_chances);
-- logging.log('v_black_winning_chances: '||v_black_winning_chances);
if (v_rec.half_move_num MOD 2 = 0)
then -- black moved
v_black_score_rate := 100 * v_score_rate;
v_white_score_rate := 100 * (1 - v_score_rate);
if (v_rec.move_black = v_rec.best_move_uci_prv) then
v_accuracy := 100.0;
v_judgement := 'ENGINE';
else
v_accuracy := calc_accuracy(v_black_winning_chances_prv, v_black_winning_chances);
v_judgement := calc_judgement(v_black_winning_chances_prv, v_black_winning_chances);
end if;
else -- white moved
v_white_score_rate := 100 * v_score_rate;
v_black_score_rate := 100 * (1 - v_score_rate);
if (v_rec.move_white = v_rec.best_move_uci_prv) then
v_accuracy := 100.0;
v_judgement := 'ENGINE';
else
v_accuracy := calc_accuracy(v_white_winning_chances_prv, v_white_winning_chances);
v_judgement := calc_judgement(v_white_winning_chances_prv, v_white_winning_chances);
end if;
end if;
v_white_draw_rate := 100 * v_draw_rate;
v_black_draw_rate := 100 * v_draw_rate;
--
-- set record data
--
v_da_position_rec.position_id := v_rec.position_id;
v_da_position_rec.white_winning_chances := v_white_winning_chances;
v_da_position_rec.white_score_rate := v_white_score_rate;
v_da_position_rec.white_draw_rate := v_white_draw_rate;
v_da_position_rec.black_winning_chances := v_black_winning_chances;
v_da_position_rec.black_score_rate := v_black_score_rate;
v_da_position_rec.black_draw_rate := v_black_draw_rate;
v_da_position_rec.accuracy := v_accuracy;
v_da_position_rec.judgement := v_judgement;
v_da_position_rec.sharpness := calc_sharpness(v_rec.wins, v_rec.losses);
--
-- upsert record
--
upsert_da_position(v_da_position_rec);
end loop;
end gen_da_position;
procedure gen_da1game (p_game_id NUMBER(20))
as
v_acpl_white double;
v_acpl_black double;
v_stdcpl_white double;
v_stdcpl_black double;
v_accuracy_avg_white double;
v_accuracy_avg_black double;
v_sum_engine_moves_white integer;
v_sum_engine_moves_black integer;
v_sum_normal_moves_white integer;
v_sum_normal_moves_black integer;
v_sum_mistake_moves_white integer;
v_sum_mistake_moves_black integer;
v_sum_blunder_moves_white integer;
v_sum_blunder_moves_black integer;
v_game_length integer;
begin
select
avg(cpl_white) acpl_white,
avg(cpl_black) acpl_black,
stddev_samp(cpl_white) stdcpl_white,
stddev_samp(cpl_black) stdcpl_black,
avg(case when cpl_white is not null then accuracy else null end) accuracy_avg_white,
avg(case when cpl_black is not null then accuracy else null end) accuracy_avg_black,
sum(case when cpl_white is not null and judgement = 'ENGINE' then 1 else 0 end) sum_engine_moves_white,
sum(case when cpl_black is not null and judgement = 'ENGINE' then 1 else 0 end) sum_engine_moves_black,
sum(case when cpl_white is not null and judgement is null then 1 else 0 end) sum_normal_moves_white,
sum(case when cpl_black is not null and judgement is null then 1 else 0 end) sum_normal_moves_black,
sum(case when cpl_white is not null and judgement = 'MISTAKE' then 1 else 0 end) sum_mistake_moves_white,
sum(case when cpl_black is not null and judgement = 'MISTAKE' then 1 else 0 end) sum_mistake_moves_black,
sum(case when cpl_white is not null and judgement = 'BLUNDER' then 1 else 0 end) sum_blunder_moves_white,
sum(case when cpl_black is not null and judgement = 'BLUNDER' then 1 else 0 end) sum_blunder_moves_black,
max(half_move_num) game_length
into
v_acpl_white,
v_acpl_black,
v_stdcpl_white,
v_stdcpl_black,
v_accuracy_avg_white,
v_accuracy_avg_black,
v_sum_engine_moves_white,
v_sum_engine_moves_black ,
v_sum_normal_moves_white,
v_sum_normal_moves_black,
v_sum_mistake_moves_white,
v_sum_mistake_moves_black,
v_sum_blunder_moves_white,
v_sum_blunder_moves_black,
v_game_length
from
(
select
t.half_move_num ,
t.move_white,
t.move_black,
t.best_move_uci,
t.centipawn,
case
when t.half_move_num mod 2 = 0 then null
else case
when t.accuracy >= 99 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_white,
case
when t.half_move_num mod 2 = 1 then null
else case
when t.accuracy >= 99 then 0
else (t.centipawn_prv - t.centipawn) * t.inverse_sign
end
end cpl_black,
t.accuracy,
t.judgement ,
t.sharpness
from
(
select
p.half_move_num ,
case
when p.half_move_num mod 2 = 1 then 1
else -1
end inverse_sign,
p.move_white ,
p.move_black ,
pa.best_move_uci ,
pa.centipawn ,
lag(pa.centipawn) over (
order by
p.game_id,
p.half_move_num ) as centipawn_prv,
dp.accuracy,
dp.judgement ,
dp.sharpness
from
chess.position p
join chess.position_analysis as pa on
p.id = pa.position_id
left outer join chess.da_position as dp on
dp.position_id = pa.position_id
where
p.game_id = p_game_id
order by
p.game_id,
p.half_move_num ) t ) t2;
insert into
da_game (game_id,
acpl_white,
acpl_black,
stdcpl_white,
stdcpl_black,
accuracy_avg_white,
accuracy_avg_black,
sum_engine_moves_white,
sum_engine_moves_black,
sum_normal_moves_white,
sum_normal_moves_black,
sum_mistake_moves_white,
sum_mistake_moves_black,
sum_blunder_moves_white,
sum_blunder_moves_black,
game_length)
values (p_game_id,
v_acpl_white,
v_acpl_black,
v_stdcpl_white,
v_stdcpl_black,
v_accuracy_avg_white,
v_accuracy_avg_black,
v_sum_engine_moves_white,
v_sum_engine_moves_black,
v_sum_normal_moves_white,
v_sum_normal_moves_black,
v_sum_mistake_moves_white,
v_sum_mistake_moves_black,
v_sum_blunder_moves_white,
v_sum_blunder_moves_black,
v_game_length);
end gen_da1game;
procedure gen_da_game
as
begin
truncate table da_game;
for v_rec in (select distinct p.game_id from da_position dap join position p on p.id =dap.position_id order by game_id)
loop
gen_da1game(v_rec.game_id);
commit;
end loop;
end gen_da_game;
end da;
//
DELIMITER ;Die Ausführungszeit der Prozedur beträgt lediglich 13 Sekunden.
Mit einer kurzen Sichtkontrolle auf die entstandenen Daten wollen wir dieses Kapitel beenden.
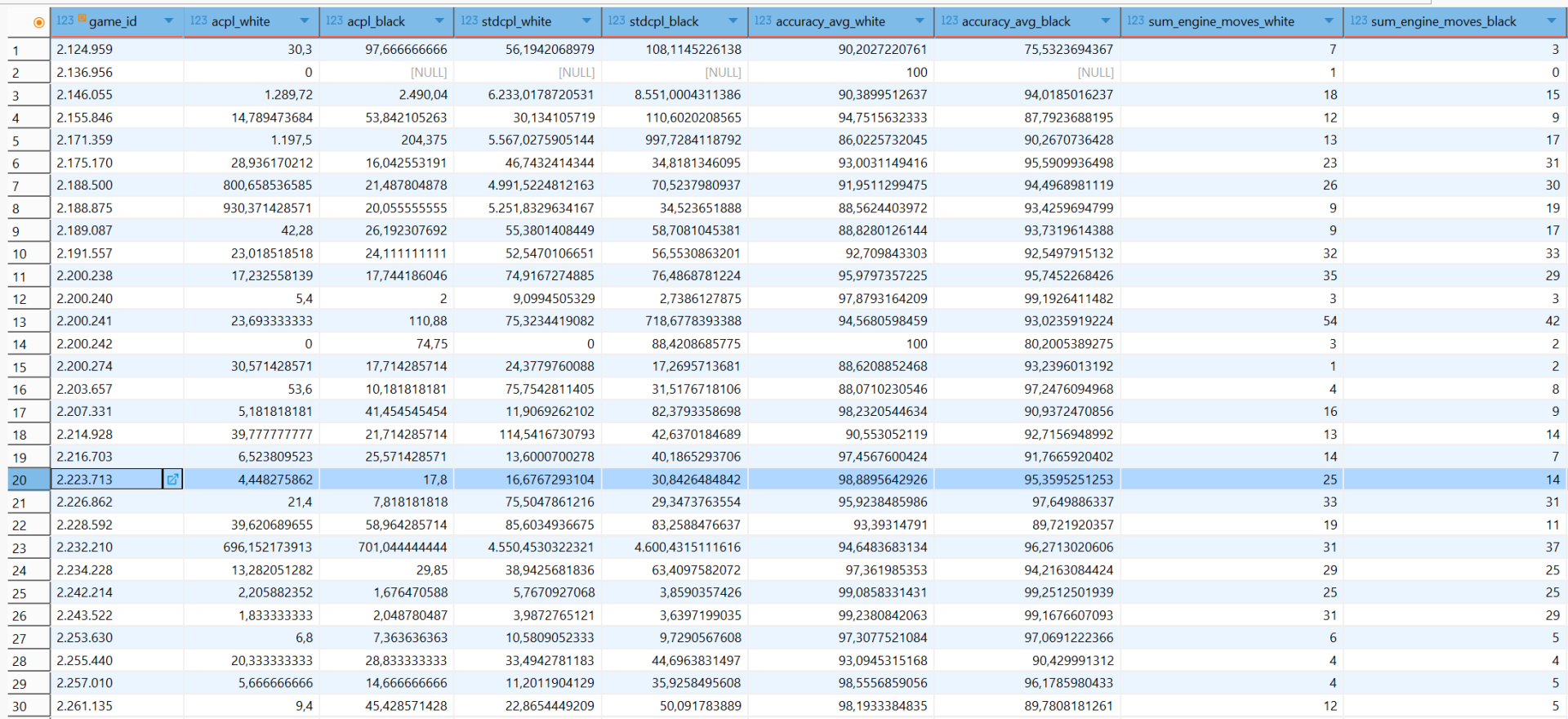
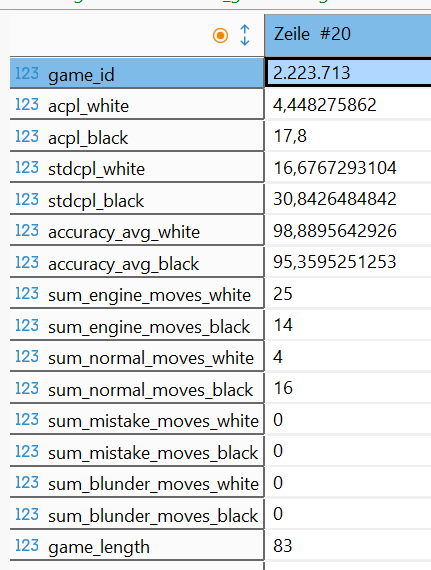
Im nächsten Kapitel beschäftigen wir uns mit der Visualisierung unserer gewonnenen Daten.


Pingback: 11) weitere Kennzahlen und Statistiken