Bevor wir in die analytischen Untiefen von Algorithmen und Software-Programmen abtauchen, wollen wir unser Vorhaben noch einmal kurz skizzieren.
von Äpfel und Birnen
Letztlich wollen wir eine Bewertung von Schachspielern anhand ihrer Partien durchführen. Diese Spieler-Bewertungen wollen wir am Ende gegeneinander vergleichen, um schlussendlich die Frage beantworten zu können, wer als bester Schachspieler aller Zeiten gelten kann.
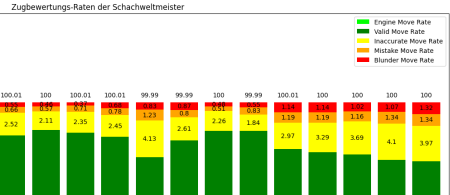
Warum zählen wir dazu nicht einfach die Ergebnisse ihrer gespielten Partien zusammen? Eine einfache Kennzahl wäre z.B. deren Gewinnquote.
Man kann anhand obiger Statistik bereits das Problem erahnen. Hier werden unterschiedliche Maßstäbe verwendet! Selbst wenn man eine vergleichbare Grundlage schafft, also z.B. nur WM-Matches oder sämtliche Spiele berücksichtigt, ist die Aussagekraft von erzielten Ergebnissen gering. Zum einen erreichen Weltklasse-Spieler ihre maximale Spielstärke in unterschiedlichen Abschnitten ihres Lebens und halten diese auch unterschiedlich lange aufrecht, abhängig von Gesundheit und Alter. Zum anderen ist die allgemeine Spielstärke heutiger Schachspieler enorm gewachsen und es ist offenkundig schwerer, gegen einen gleichwertigen Gegner zu gewinnen, der ebenfalls mit dem gesamten verfügbaren Wissen über Schachtheorie und Eröffnungssysteme ausgestattet ist. Der Graben zwischen den Spielstärken heutiger Großmeistern ist weniger tief als von 100 Jahren.
Das Hauptproblem bei der bloßen Berücksichtigung von Spielergebnissen ist, dass sie kein absoluter Bewertungsmaßstab sein können, sondern immer in Relation zum jeweiligen Gegner stehen.
Wie können wir also Vergleichbarkeit und Objektivität herstellen? Um das Phänomen der individuellen Leistungskurven von Spielern zu berücksichtigen, kann man z.B. die Kennzahlen jahresbezogen ermitteln. Und um die unterschiedlichen Spielstärken der Gegner zu berücksichtigen, lässt sich die Qualität von deren Züge ebenfalls ermitteln und gegenrechnen. Mit den richtigen Metriken kann man sogar Simultan- oder Vorgabe-Partien gleichfalls bewerten. Wie das genau funktioniert, sehen wir später.
Analyse und Metrik
Es ist klar, dass wir uns für eine Spielerbewertung dessen Partien ansehen müssen. Und um eine Schachpartie zu bewerten, müssen wir sowohl die Züge des betreffenden Spielers wie auch dessen Gegners betrachten. Damit kommen wir zum Thema der Metrik.
Die Bewertung von Schachstellungen vor und nach einem Zug hat eine lange Geschichte und hat vielfältige Facetten. Wir wollen das hier nicht ausführlich darstellen. Auch wenn Materialvorteil nur ein Aspekt bei der Stellungsbewertung ist, war dieser Maßstab seit langem etabliert, da er im Gegensatz zu Tempo- oder Positions-Vorteilen leicht quantifizierbar ist. Ausgehend von den relativen Figurenwerten untereinander hat sich historisch folgende Metrik als Quasi-Standard herausgebildet.
Der Spielfigur des Bauern wird hier der geringste Wert zugemessen und folglich bildet er die Einheit dieser Metrik. Dieser Bewertungsmaßstab hat den Vorteil, dass durch bloßen Figuren-Vergleich zwischen Weiß und Schwarz und Aufsummieren von deren Werten eine leicht berechenbare Metrik ergibt. In vielen positionell ausgeglichenen Stellungen ergibt diese Metrik auch Sinn. Die bevorzugte Strategie für den Spieler mit Materialvorteil ist meist, so viele Figuren wie möglich mit dem Gegner abzutauschen, denn um so deutlicher kann dieser Vorteil im Endspiel zum Sieg genutzt werden.
Die Schattenseite dieser Metrik wird in der nachfolgenden Position aus einer berühmten Partie von Paul Morphy deutlich:
Obwohl Weiß materiell hoffnungslos unterlegen ist, setzt er Schwarz in nächsten Zug Schachmatt!
Materialvorteil allein ist damit offenkundig kein geeigneter Maßstab und so wird in der Praxis eine Vielzahl weiterer Kriterien, vor allem positionelle Aspekte, in das Kalkül integriert. Doch wie soll man damit rechnen? Wie ist z.B. bei Materialgleichheit ein isolierter Bauer im gegnerischen Lager mit dessen Raumvorteil gegenzurechnen? Kann man dafür einen numerischen Wert errechnen?
Dieses Problem wurde spätestens mit dem Aufkommen der ersten Schachprogramme greifbar, denn Computer können nun einmal am besten Zahlen vergleichen. Und so ist man hier wieder zur bewährten Bauern-Einheit zurückgekehrt, doch nutzt man diese heute nicht mehr nur zur Messung des Materialverhältnisses, sondern gesamthaft für sämtliche Aspekte einer Stellungsbewertung. Darüber hinaus wurde der Maßstab weiter verfeinert, indem in Hundertstel von Bauern-Einheiten gerechnet wird (im Fachjargon centipawns).
Doch während diese Einheit für die interne Stellungs-Bewertung eines Schachprogrammes genügt, ist sie als bloße Zahl schwer interpretierbar. Als menschlicher Spieler bin ich mehr daran interessiert, wie hoch meine Wahrscheinlichkeit ist, die Partie zu gewinnen bzw. zu verlieren.
Für einen einzelnen Zug hätte man gerne eine leicht verständliche Bewertungsmetrik zur Hand, etwa wie sie der wegweisende Schachinformator 1966 eingeführt hatte:
Und so geschah es – während die heutigen Schachprogramme meist noch centipawn-Bewertungen liefern, sind die einflussreichen Schach-Communities wie lichess.org und chess.com seit geraumer Zeit dazu übergegangen, diese Metrik zu erweitern und zu ergänzen (siehe auch die Genauigkeits-Metrik von Lichess und das expected points model von chess.com).
Damit haben wir nun folgende Werkzeuge zur Hand:
- die centipawns-Metrik als absolutes numerisches Maß (nicht ganz, aber darauf kommen wir noch zu sprechen)
- daraus abgeleitet die Gewinnwahrscheinlichkeit für einen Zug zwischen 0 und 100 Prozent.
- ebenfalls daraus abgeleitet die Genauigkeit eines Zuges in Hinblick auf die Abweichung vom jeweils besten Zug, der aus Sicht des Schachprogramms möglich gewesen wäre. Diese Metrik wir heute gerne zur Durchführung von Anti-Betrugs-Maßnahmen verwendet.
- Zug-Klassifikation nach obiger oder einer ähnlich sprechenden Nomenklatur.
