Im vorherigen Artikel zur Analyse einer Beispiel-Partie haben wir bereits erfahren, dass wir uns auf die Stellungsbeurteilung von Schachprogrammen nicht immer zu 100% verlassen können. Selbst mit sehr langer Bedenkzeit und großer Rechentiefe sind Fehlurteile möglich. Zudem war unser Beispiel der Opernhaus-Partie insofern nicht sehr repräsentativ für aktuelle Wettkampfpartien auf höchstem Niveau, als dass die Partie mehr taktisch als strategisch geprägt war und bereits in der Eröffnung etliche Schnitzer vom Nachziehenden begangen wurden. In solchen Situationen entstehen oft forcierte Zugfolgen, mit denen ein Schachprogramm leichter umgehen und bessere Vorhersagen über den Partie-Ausgang treffen kann.
Wenn wir also ausgewogene Parameter für Rechenzeit und maximaler Suchtiefe festlegen wollen, müssen wir auch moderne, strategisch angelegte Partien untersuchen, in denen beide Seiten selten schwere Fehler begehen. Wir werden weiter unten solch eine Partie ebenfalls testen.
So schnell heutige Computer auch rechnen können, müssen wir trotzdem einen pragmatischen Kompromiss zwischen erwünschter Genauigkeit der Analyse und erträglichem Aufwand dafür finden. Immerhin wollen wir nicht nur einzelne Partien, sondern nahezu sämtliche Partien von vielen Spielern untersuchen.
Außerdem wollen wir alle Stellungen mit dem selben Augenmerk, sprich mit gleichen Mitteln prüfen. Es wäre nicht korrekt, eine Partie nur oberflächlich und eine andere dagegen mit immenser Rechenpower zu analysieren.
Einen großen Unterschied macht selbstverständlich die konkrete Hardware-Ausstattung, z.B. die Art und Anzahl der CPU-Kerne oder des verfügbaren Arbeitsspeichers. Glücklicherweise liefern die meisten Schachprogramme neben den eigentlichen Analyse-Kennzahlen auch statistische Informationen zurück, z.B. zur Rechenzeit, Suchtiefe und Anzahl der untersuchten Varianten. Wir wollen daher einige dieser statistischen Größen zusammen mit den Kennzahlen dokumentieren, um auch über die Qualität der Berechnungen auskunftsfähig zu sein. Damit lassen sich unsere Ergebnisse objektiv mit alternativen Analysen von anderer Seite vergleichen.
Die Kennzahlen
Wir haben im Kapitel über Metriken zur Spielanalyse Kennzahlen wie Genauigkeit, Spielschärfe oder Brillanz identifiziert, die uns gesamthaft möglichen sollen, Aufschluss über z.B. Spielstärke oder Risikobereitschaft eines Schachmeisters zu geben.
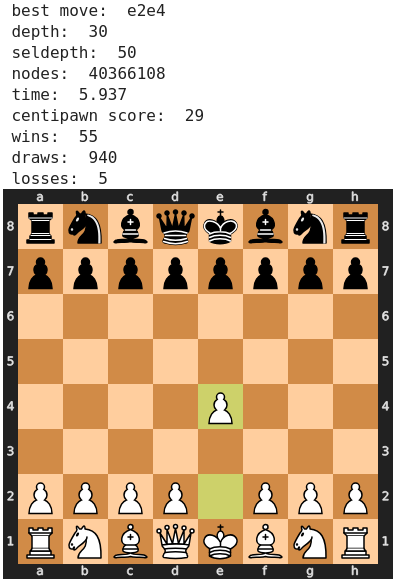
Bei genauerer Betrachtung sind alle diese Kennzahlen lediglich von der absoluten centipawn-Metrik und der Win-Draw-Loss-Metrik abgeleitet. Glücklicherweise liefert unser Python chess-Modul auf Basis der Stockfish chess engine beide Daten frei Haus!
import chess
...
mate_centipawns = 32000
info = engine.analyse(board, search_limit)
eng_score = info.get("score")
centipawn_score = eng_score.white().score(mate_score=mate_centipawns)
print ("centipawn score: ", centipawn_score)
wdl = eng_score.wdl()
wins, draws, losses = wdl[0], wdl[1], wdl[2]
print ("wins: ", wins)
print ("draws: ", draws)
print ("losses: ", losses)
Als Teil des Analyse-Ergebnisses können wir uns auch den besten gefundenen Zug zurückliefern lassen. Diesen wollen wir neben dem centipawn- und den drei win/draw/loss-Werten ebenfalls in unserer Datenbank speichern. Wir können damit später z.B. eine Aussage darüber treffen, in wie vielen Fällen ein bestimmter Spieler die besten Züge aus Sicht der Maschine tatsächlich gespielt hat.
Wir könnten uns darüber hinaus noch weitere alternative Züge von der engine liefern lassen, ebenfalls mit deren Bewertungszahlen. Allerdings verzichten wir darauf und beschränken uns auf die Hauptvariante mit dem besten Zug, da die Berechnung von Nebenvarianten wertvolle Ressourcen bindet, die wir dafür nicht verschwenden wollen.
Wie oben angesprochen wollen wir als Beifang noch statistische Werte sammeln und speichern, konkret sind dies
- depth (Suchtiefe in Anzahl Halbzüge)
- seldepth (Suchtiefe in Anzahl Halbzüge für Hauptvariante)
- nodes (Anzahl der untersuchten Stellungen)
- time (verbrauchte Computer-Rechenzeit in Sekunden)
Im Ergebnis speichern wir also pro analysierter Stellung diese Werte in unserer Analyse-Datenbank.
Festlegungen zur Parametrisierung
Wir können unsere chess engine Stockfish in zweierlei Hinsicht parametrisieren.
Hardware-Parameter
Zum einen verwenden wir zwei Stellschrauben, um die vorhandene Hardware optimal zu nutzen. Dies geschieht über Einstellungen der Parameter Threads und Hash. Diese beziehen sich auf die Kapazitäten bei den CPU-Kernen und dem vorhandenen Hauptspeicher (RAM).
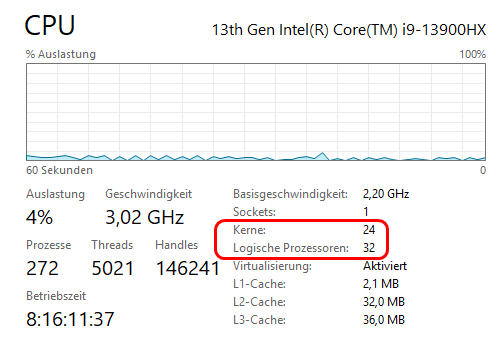
Stockfish empfiehlt für eine optimale Performance, die Anzahl Threads auf die maximale Anzahl der vorhandenen logischen Prozessoren zu setzen, abzüglich 1 oder 2 für andere Aufgaben. In unserem Fall sollte daher Threads=30 ein brauchbarer Wert sein.
Was den Parameter Hash angeht, also die Nutzung des Hauptspeichers als Cache, gilt die Faustregel „so viel wie möglich, ohne Beeinträchtigung des Betriebssystems“. In unserem Fall mit 64GB Hauptspeicher, sollten daher 48GB Hash leicht möglich sein.
Engine-Parameter
Würden wir der chess engine bei ihrer Analyse keinerlei Einschränkungen auferlegen, würde sie in den allermeisten Positionen bis zum Ende der Welt rechnen. Die Zeit und das Geld dafür haben wir nicht. Deshalb sind wir gezwungen, Vorgaben für die Rechendauer und die maximale Suchtiefe zu machen. Andererseits wollen wir aber auch gute Ergebnisse in komplizierten und strategisch geprägten Stellungen erzielen.
Zu diesem Zweck wollen wir einen Testlauf mit einer Parametrisierung durchführen, die einerseits noch zu guten Ergebnissen führt und andererseits von ihrem Laufzeitverhalten akzeptabel bleibt.
Wir wählen dabei eine bekannte und hinreichend analysierte Schachpartie aus, die darüber hinaus einen strategischen Charakter mit verwickelten Varianten aufweist. Prüfen wollen wir dabei vor allem einige ausgewählte Schlüsselpositionen, an denen wir die Analyse-Ergebnisse der engine bewerten können. Wir wählen zu diesem Zweck die allseits bekannte 13. Partie aus dem Weltmeisterschaftskampf Fischer-Spasski von 1972 in Reykjavik aus.
Als Anfangsparametrisierung legen wir für die Suchtiefe und Rechenzeit in Sekunden den Wert 30 fest. Sind wir mit den Ergebnissen zufrieden, versuchen wir im zweiten Schritt, die maximale Rechenzeit weiter zu verkürzen, so dass die Ergebnisse aber immer noch akzeptabel bleiben.
Wir nutzen das unten stehende Python-Programm in einem Jupyter-Notebook, bei dem wir die Hardware-Parametrisierung etwas drosseln, da das Jupyter-Notebook aus den bekannten Gründen in einer VM mit eingeschränkten Hardware-Ressourcen läuft.
Neben der Ermittlung und Anzeige der Kennzahlen centipawn und wdl zeigen wir der Anschauung halber bereits daraus abgeleitete Werte zu den Gewinnwahrscheinlichkeiten an. Wir greifen hier bewusst voraus, um die nackten Kennzahlen verständlicher zu gestalten.
Python Code
import chess
import chess.engine
import chess.pgn
from IPython.display import Image, display
# performance tuning parameters
num_threads=14 #20
hash_mb=24000 #48000
# analysis limits
max_depth = 30
movetime_sec = 30
num_moves_to_return = 1
mate_centipawns = 32000
engine_path = "/home/peterk/stockfish/stockfish-ubuntu-x86-64-avx2"
engine = chess.engine.SimpleEngine.popen_uci(engine_path)
engine.configure({'Threads':num_threads, "Hash": hash_mb})
def analyze_position(fen, move):
search_limit = chess.engine.Limit(depth=max_depth, time=movetime_sec)
board = chess.Board(fen, chess960=False)
stm = board.turn
info = engine.analyse(board, search_limit) # , game=object()
print (info)
print ("----------------------")
# print move played
print ("played move: ", move.uci())
# print best move
best_move = info["pv"][0].uci()
print ("best move: ", best_move)
depth=info["depth"]
print ("depth: ", depth)
seldepth=info["seldepth"]
print ("seldepth: ", seldepth)
nodes=info["nodes"]
print ("nodes: ", nodes)
time=info["time"]
print ("time: ", time)
# print score and wdl
eng_score = info.get("score")
if eng_score is not None:
centipawn_score = eng_score.white().score(mate_score=mate_centipawns)
print ("centipawn score: ", centipawn_score)
# print wdl
wdl = eng_score.wdl() # win/draw/loss info point of view is stm
wins, draws, losses = wdl[0], wdl[1], wdl[2]
print ("wins: ", wins)
print ("draws: ", draws)
print ("losses: ", losses)
score = wins + draws/2
total = wins + draws + losses
score_rate = score / total
win_rate = wins / total
draw_rate = draws / total
loss_rate = losses / total
white_winning_chances = win_rate if stm==chess.WHITE else loss_rate
black_winning_chances = win_rate if stm==chess.BLACK else loss_rate
white_score_rate = score_rate if stm==chess.WHITE else 1 - score_rate
black_score_rate = score_rate if stm==chess.BLACK else 1 - score_rate
# Show info.
print(f'white_winning_chances: {100 * white_winning_chances:0.2f}%, white_score_rate: {100 * white_score_rate:0.2f}%, white_draw_rate: {100 * draw_rate:0.2f}%')
print(f'black_winning_chances: {100 * black_winning_chances:0.2f}%, black_score_rate: {100 * black_score_rate:0.2f}%, black_draw_rate: {100 * draw_rate:0.2f}%')
with open("../data/fischer_spasski_13.pgn", encoding="utf8") as pgn:
game = chess.pgn.read_game(pgn)
board = game.board()
for move in game.mainline_moves():
if not board.outcome():
analyze_position(board.fen(), move)
board.push(move)
display(board)
engine.quit()Wir überspringen die ersten Züge aus dem Eröffnungsbuch, die auch Analyse-seitig keine Überraschungen aufweisen und gelangen zur Position vor dem siebten Zug von Weiß.
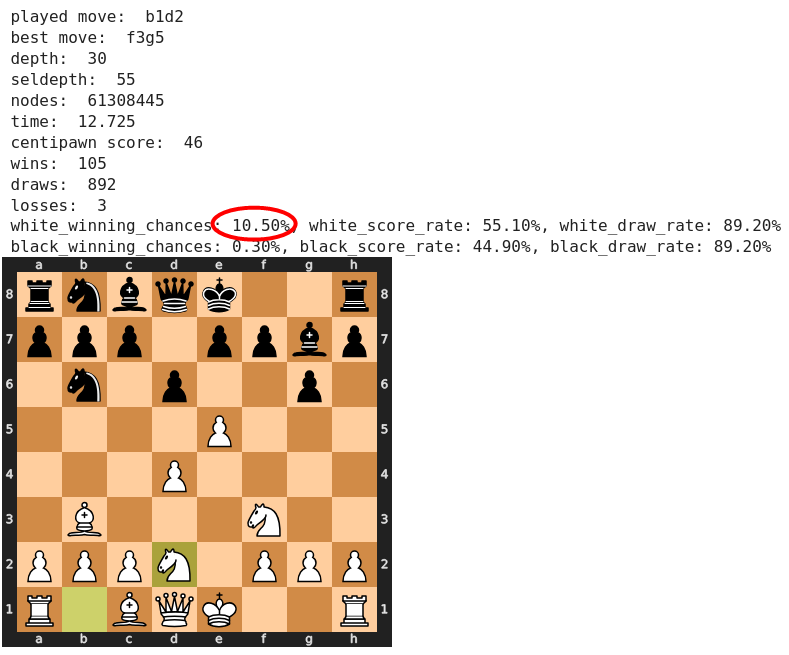
Mit dem von Stockfish errechneten besten Zug 7) Sg5 besteht eine Gewinnwahrscheinlichkeit von 10,5% für Weiß. Der tatsächlich von Spasski gespielte und allgemein als zu passiv kritisierte Zug 7) Sb1-d2 führt zu einer Stellung, in der sich die Gewinnwahrscheinlichkeit auf die Hälfte reduziert. Dies klingt Analyse-seitig auch plausibel.
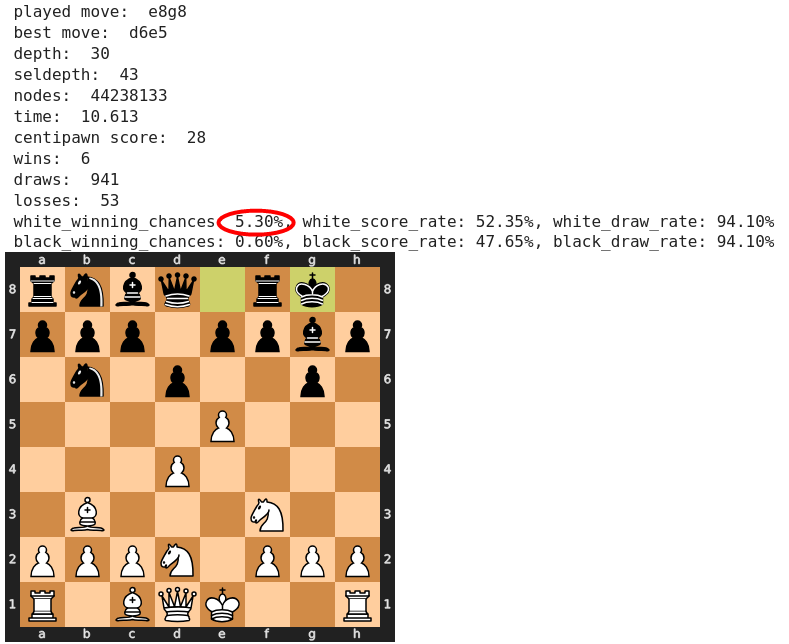
Zwei Züge später spielt Weiß seinen Bauer auf a4, wo er ihn wenig später fast zwangsläufig einbüßen muss. Dass Stockfish ausgerechnet diesen als besten Zug empfiehlt, überrascht auf den ersten Blick.
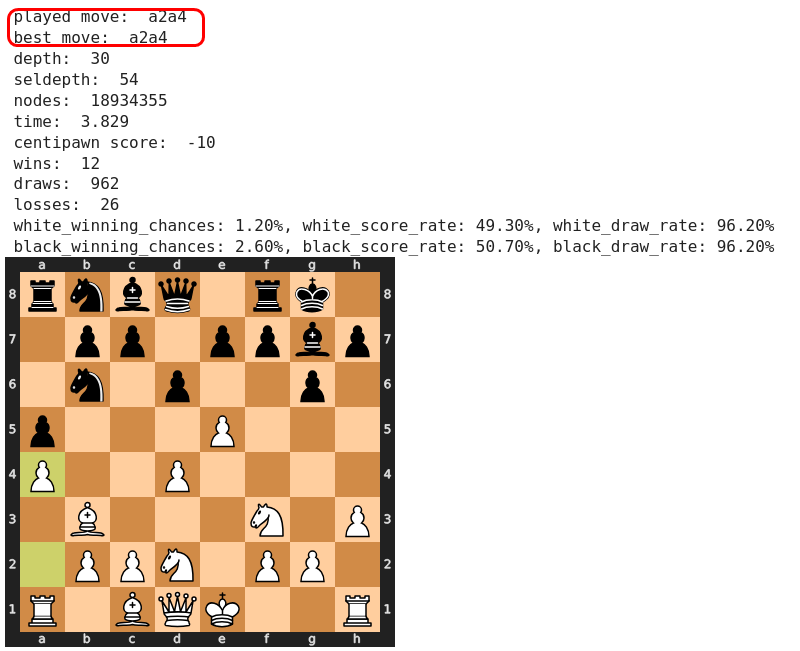
Tatsächlich aber erhält Weiß ausreichend Kompensation für den verlorenen Bauern, so dass Stockfish auch hier richtig liegt. Allerdings ist dieser Zug auch sehr verpflichtend, denn Weiß muss in der Folge sehr genau und aktiv spielen, um Ausgleich zu erzielen. Dies ist ein klarer psychologischer Nachteil, den Stockfish hier aber nicht berücksichtigen kann!
Wir springen nun zum achtzehnten Zug von Schwarz 18) …, Lf5, der allgemein als ungenau bewertet wurde mit der empfohlenen Alternative 18) …, Ld7. Sehen wir uns die Beurteilung durch Stockfish an.
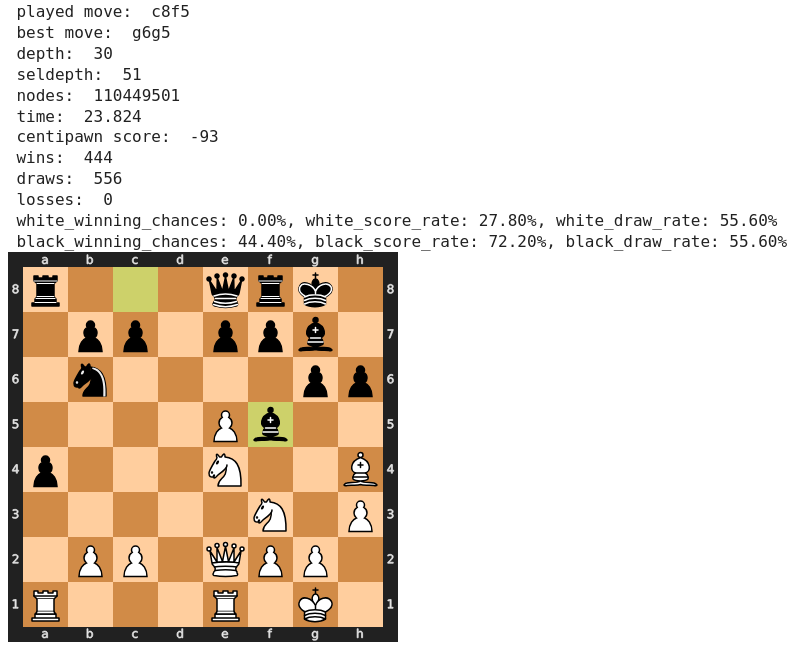
anhand der Folgestellung sehen wir, dass Fischer’s Zug erstens zu keiner wesentlichen Verschlechterung seiner Stellung führt und zweitens Stockfish nicht etwa 18) …, Ld7, sondern 18) …, g5 als besten Zug empfiehlt.

Es ist vielmehr der Folgezug 19) g4, den Stockfish als schlecht für Weiß beurteilt. Interessant, aber keineswegs abwegig.
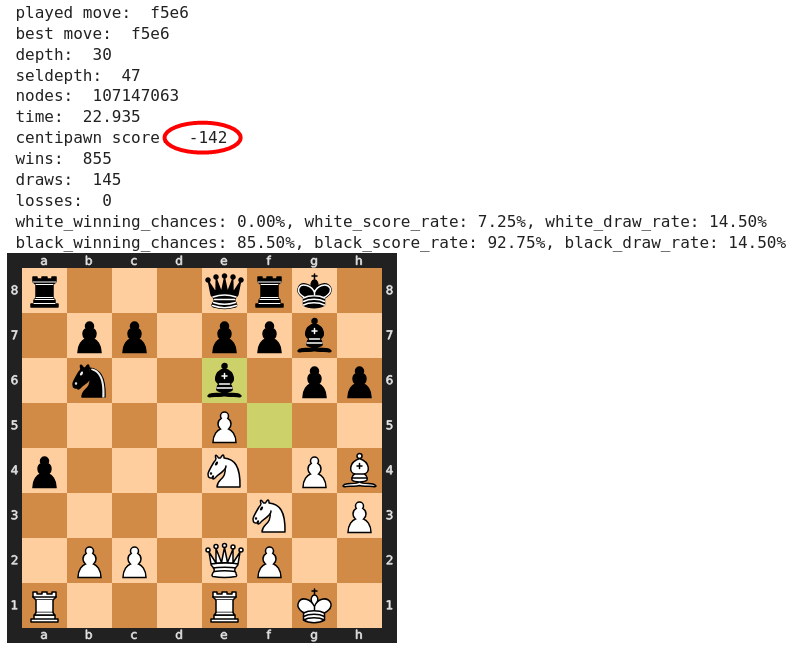
Der nächste Zug von Weiß 20) Sd4! wird allgemein gelobt, doch Stockfish zieht den unscheinbar wirkenden Zug 20) Dd3 vor. Immerhin attestiert der Computer Sd4 keine wesentliche Stellungsverschlechterung.
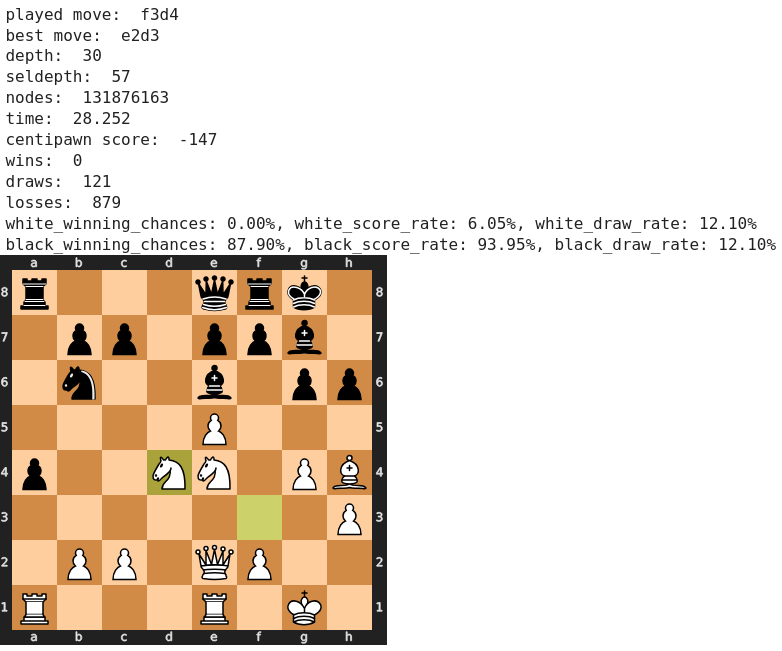
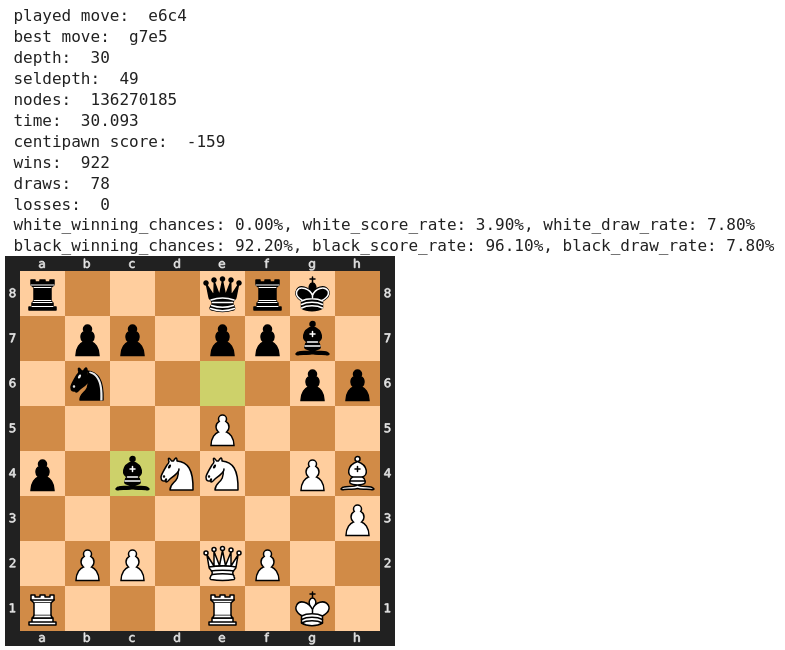
Wir gelangen direkt zu 27) Sd3, ein Zug, der kritisiert wurde, da Schwarz nun den Übergang in ein Endspiel mit einem Mehrbauern forcieren kann. Stockfish favorisiert hier ebenfalls den als gute Alternative empfohlenen Zug 27) Sb5. Allerdings verbliebe Weiß auch damit in der schlechteren Stellung.
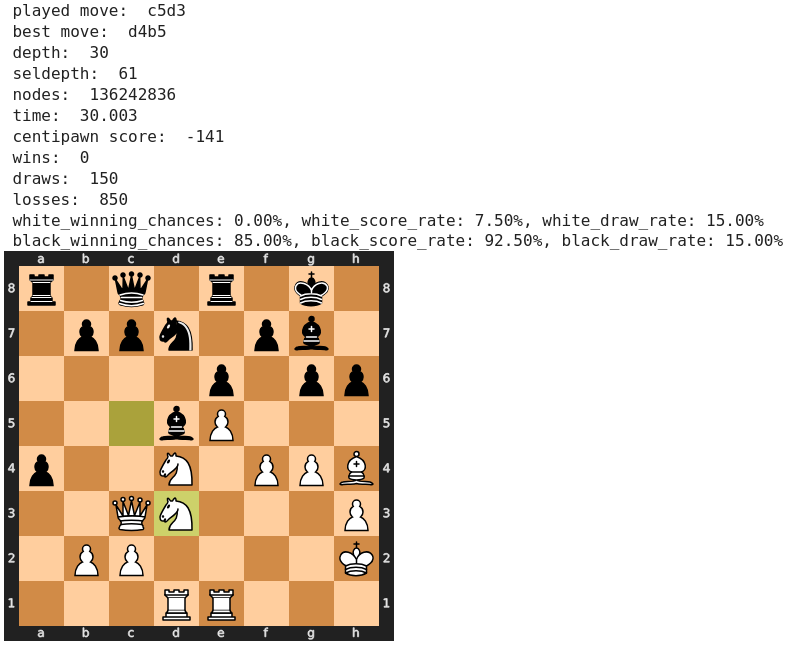
Der Zug 32) g5! wurde ebenfalls gelobt, da er die „dunklen Felder im schwarzen Lager schwächt“. Stockfish kann dieser Beurteilung nichts abgewinnen und empfiehlt stattdessen 32) Ta1, wobei Spasski’s Zug aber auch zu keiner nennenswerten Verschlechterung führt.
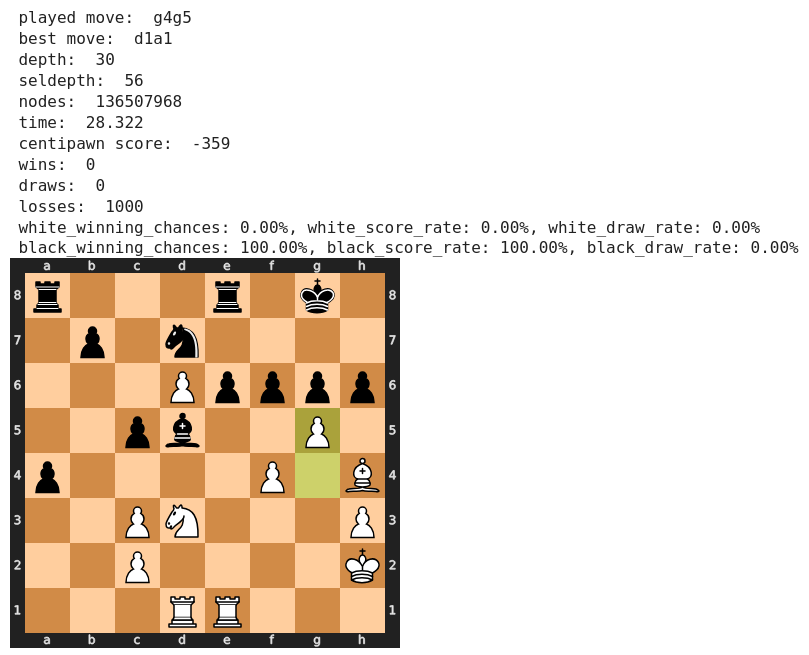
in beiden Fällen liegt die Gewinnwahrscheinlichkeit für Schwarz bereits bei 100% !
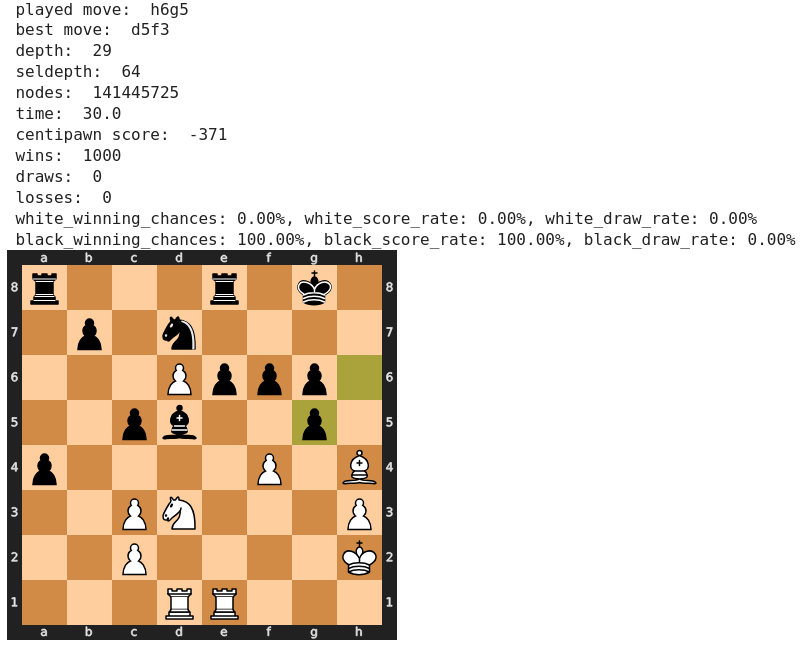
Gehen wir weiter zu 36) …, b5. Dieser Zug wird in den Kommentaren nicht einhellig kritisiert. Auf zum Beispiel chessbase.com wird er kommentarlos wiedergegeben, auf chess.com dagegen etwas kritisiert.
Bei Stockfish hingegen steigt der centipawn-Wert im Vergleich zu seiner eigenen Empfehlung 36) …, Te8-d8 schlagartig von -215 auf -63.
Die Gewinnwahrscheinlichkeit für Schwarz sinkt entsprechend von 99% auf nur noch 19%.
Dass dieser Zug von den Analysten nicht klar genug gebrandmarkt wurde liegt eventuell daran, dass Spasski im Folgezug selbst patzte, womit die Gewinnchancen für Schwarz sofort wieder erhöht werden.

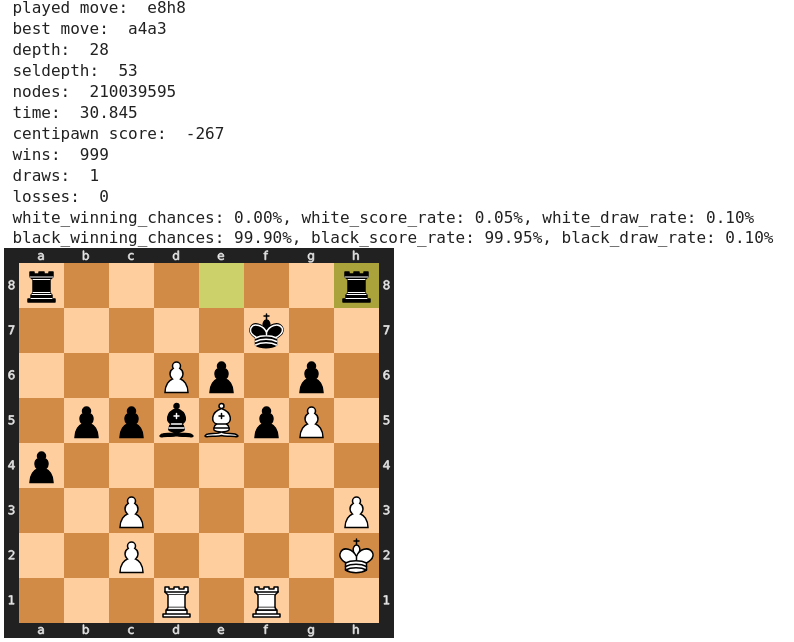
Beim gelobten Abgabezug 42) Kg3! von Boris Spasski sind sich der maschinelle und die menschlichen Analysten in ihrer Bewertung wieder völlig einig.

Dass 43) …, Th8-a8, mit dem Fischer bedingungslos auf Gewinn spielt, ebenfalls als bester Zug bewertet wird, erscheint uns genauso korrekt.
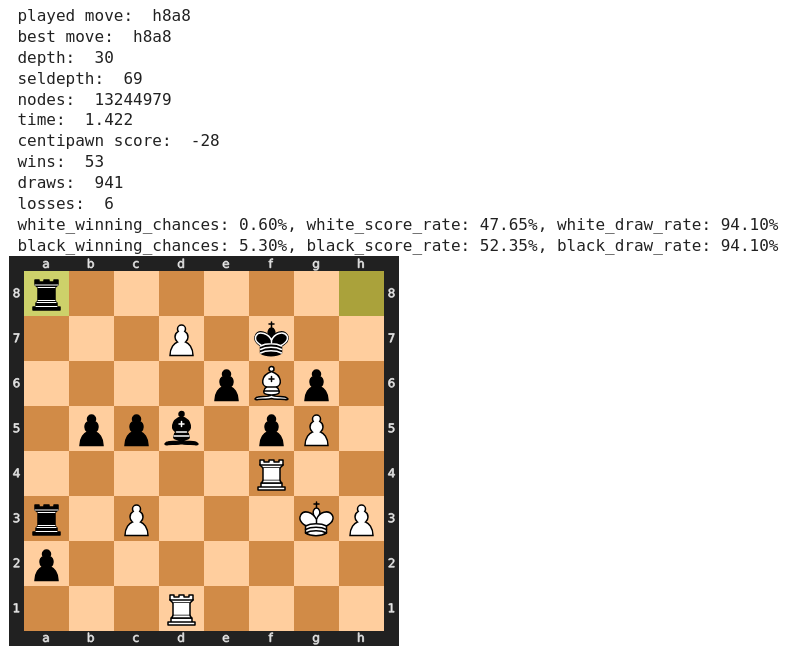
Alle folgenden Bewertungen durch Stockfish wirken durchweg plausibel, so dass wir nun einen großen Sprung zu Spasski’s Verlustzug 69) Td1 machen. Wir wollen wissen, ob Stockfish dies erkennt und ob er den einzig möglichen Rettungszug findet.
Tatsächlich findet Stockfish bereits nach 0,09 Sekunden den rettenden Zug!
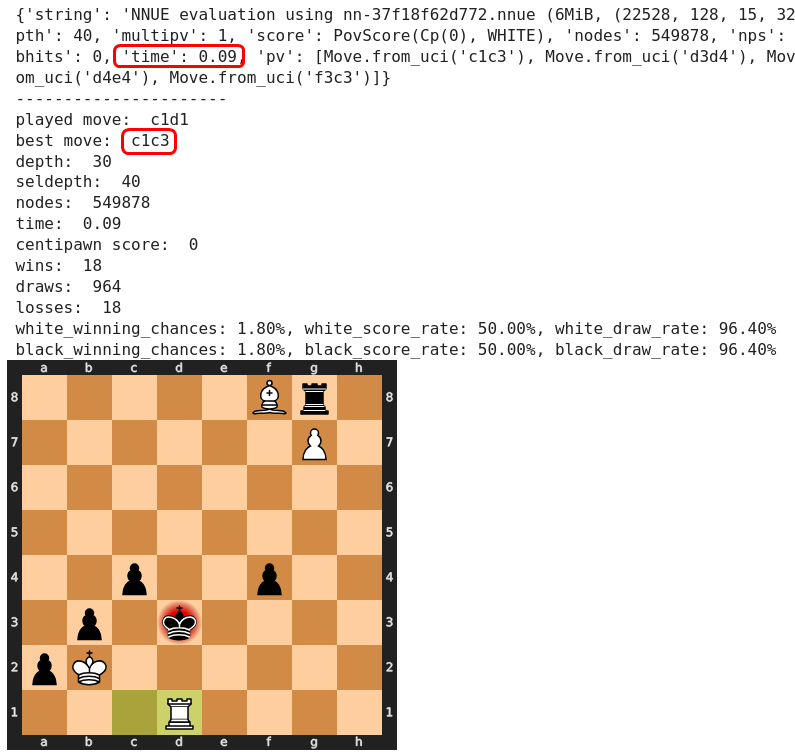
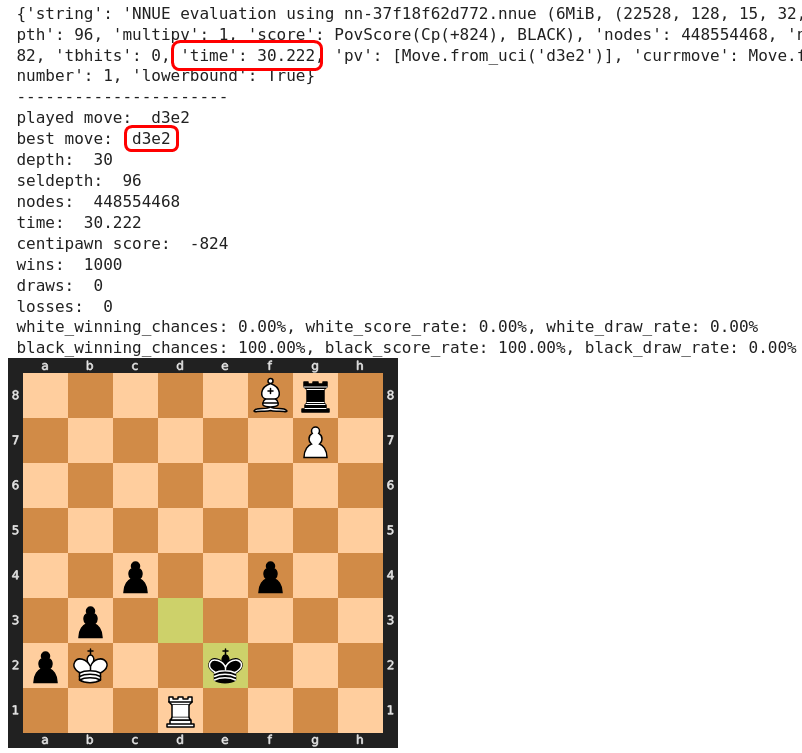
und genauso treffsicher (wenn auch nicht so schnell) findet Stockfish den nachfolgenden Gewinnzug für Schwarz.
Zwischenfazit
Der Test erfüllt unsere Erwartungen, auch wenn der Umfang mit lediglich zwei Partien eher dürftig erscheinen mag. Doch unsere Ressourcen sind begrenzt und die Analyse einer einzigen Partie mit wie hier fast 80 Zügen verschlingt ca. 40 Minuten an Rechenzeit! So wollen wir prüfen, ob wir den Zeitbedarf noch weiter drosseln können, indem wir z.B. die zugestandene CPU-Zeit halbieren. Probieren geht über Studieren…
Zweiter Lauf
Wir überprüfen obige Stichproben nun mit der reduzierten Rechenzeit von 15 Sekunden. Die maximale Suchtiefe von 30 Halbzügen lassen wir hingegen bestehen.
Der Übersichtlichkeit halber fassen wir die Ergebnisse an den oben besprochenen Schlüsselstellen in einer Tabelle zusammen.
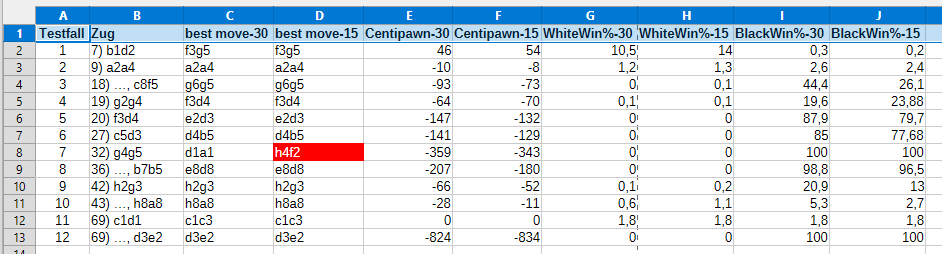
Wenn man von den relativ geringfügigen Abweichungen bei den numerischen Bewertungszahlen absieht, differiert das Ergebnis bezüglich der Zugempfehlungen nur an einer Stelle. Sehen wir uns diese Position genauer an, indem wir Stockfish eine noch tiefere (depth=42) Baumsuche erlauben.
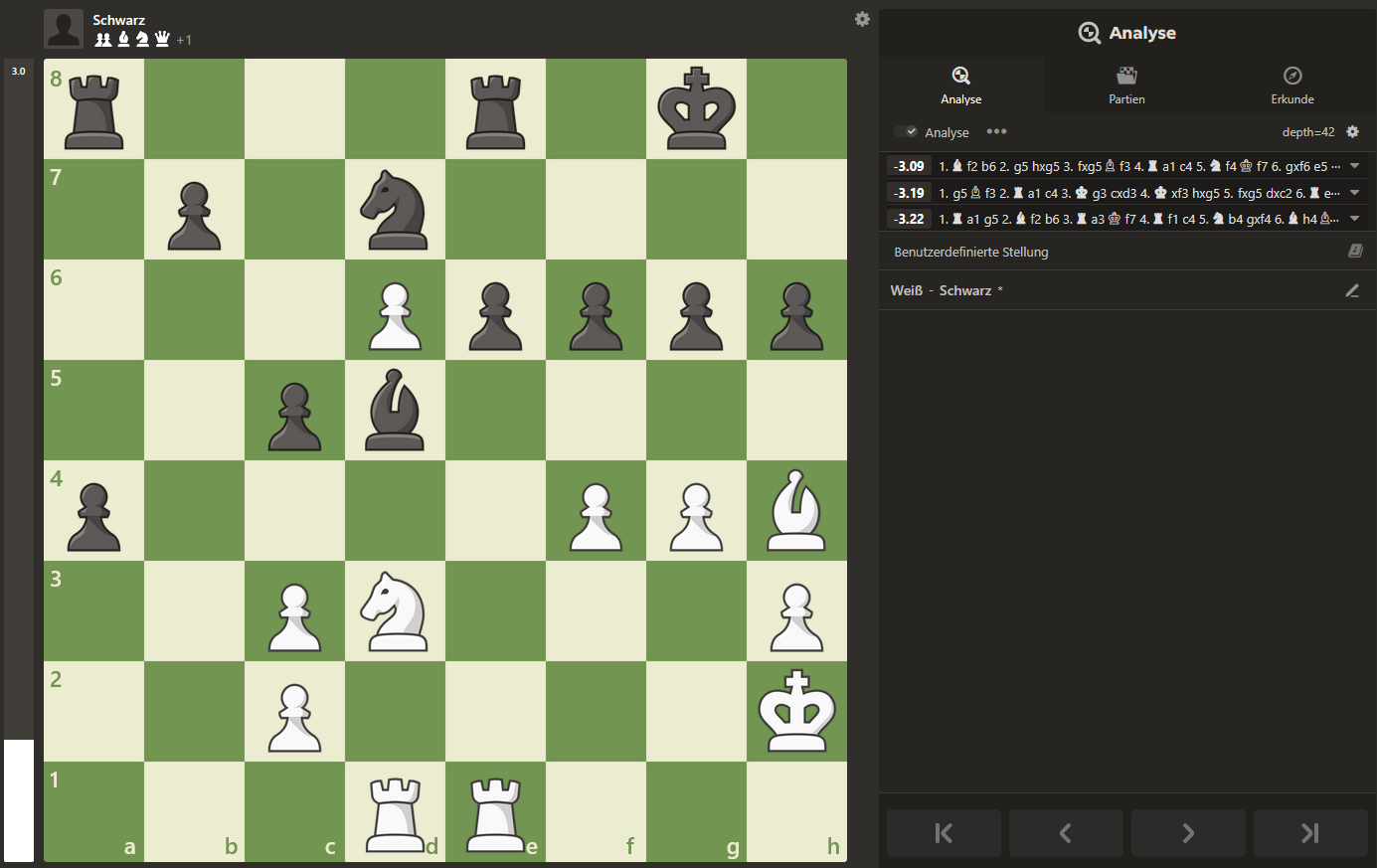
Das Ergebnis ist höchst interessant! Man kann während der Berechnung live beobachten, wie im Laufe der Baumsuche, während der die Suchtiefe stetig ansteigt, sich der Centipawn-Wert ständig zusammen mit der jeweiligen Rangordnung der Zugempfehlung ändert. Es ist daher anzunehmen, dass sich dieses Verhalten bei höherer Rechentiefe noch fortsetzt. Stabil bleiben hingegen die geringen Bewertungs-Unterschiede zwischen den Zug-Favoriten, so dass wir bereits mit den Ergebnissen der verkürzten Analyse über 15 Sekunden zufrieden sein können. Da wir auch mit einer 15-tägigen Berechnungszeit pro Zug noch keine Gewähr haben, den wirklich besten Zug gefunden zu haben, belassen wir es bei dieser Einstellung. Sollte jemand über die nötigen Ressourcen für längere Rechenzeiten verfügen, z.B. durch eine Cloud-Installation mit hohem Parallelisierungsgrad, darf er eine tiefere Analyse anhand unserer Software gerne wiederholen.

Pingback: 11) weitere Kennzahlen und Statistiken